IFFT
Inverse fast Fourier transform (IFFT) of input
Libraries:
DSP System Toolbox /
Transforms
Description
The IFFT block computes the inverse fast Fourier transform (IFFT) across the
first dimension of an N-D input array. The block uses one of two
possible FFT implementations. You can select an implementation based on the FFTW library
or an implementation based on a collection of Radix-2 algorithms. To allow the block to
choose the implementation, you can select Auto. For more
information about the FFT implementations, see Algorithms.
When you specify an FFT length not equal to the length of the input vector (or first dimension of the input array), the block implements zero-padding, truncating, or modulo-M (FFT length) data wrapping. This occurs before the IFFT operation. For an IFFT with P ≤ M:
y = ifft(u,M) % P ≤ MWrapping:
y(:,L) = ifft(datawrap(u(:,L),M)) % P > M; L = 1,...,NTruncating:
y (:,L) = ifft(u,M) % P > M; L = 1,...,NTip
When the input length, P, is greater than the FFT length, M, you may see magnitude increases in your IFFT output. These magnitude increases occur because the IFFT block uses modulo-M data wrapping to preserve all available input samples.
To avoid such magnitude increases, you can truncate the length of your input sample, P, to the FFT length, M. To do so, place a Pad block before the IFFT block in your model.
Examples
Ports
Input
Port_1 — Input signal
vector | matrix | N-D array
Input signal for computing the IFFT. The block computes the IFFT along the first dimension of the N-D input signal. The input can be floating-point or fixed-point, real, or complex, and conjugate symmetric.
For more information on how the block computes the IFFT, see Description and Algorithms.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Complex Number Support: Yes
Output
Port_1 — IFFT of input
vector | matrix | N-D array
The IFFT, computed across the first dimension of an N-D input array. For more information on how the block computes the IFFT, see Description and Algorithms.
The kth entry of the Lth output channel, y(k,L), is equal to the kth point of the M-point inverse discrete Fourier transform (IDFT) of the Lth input channel:
The output has the same dimensions as the input. If the input signal has a floating-point data type, the data type of the output signal uses the same floating-point data type. Otherwise, the output can be any signed fixed-point data type. The block computes scaled and unscaled versions of the IFFT.
Data Types: single | double | int8 | int16 | int32 | fixed point
Parameters
Main
FFT implementation — FFT implementation
Auto (default) | Radix-2 | FFTW
Set this parameter to FFTW to support an
arbitrary length input signal. The block restricts generated code with
FFTW implementation to MATLAB® host computers.
Set this parameter to Radix-2 for bit-reversed processing,
fixed or floating-point data, or portable C-code generation using the
Simulink®
Coder™. The dimension M of the
M-by-N input matrix, must be a
power of two. To work with other input sizes, use the Pad block to pad or truncate
these dimensions to powers of two, or if possible choose the FFTW
implementation. For more information about the algorithms used by the
Radix-2 mode, see Radix-2 Implementation.
Set this parameter to Auto to let the block
choose the FFT implementation. For floating-point inputs with
non-power-of-two transform lengths, the FFTW algorithm is automatically
chosen. Otherwise a Radix-2 algorithm is automatically chosen. For
non-power-of-two transform lengths, the block restricts generated code
to MATLAB host computers.
Input is in bit-reversed order — Input is in bit-reversed order
off (default) | on
Select or clear this check box to designate the order of the input channel elements. Select this check box when the input is in bit-reversed order, and clear it when the input is in linear order. The block yields invalid outputs when you do not set this parameter correctly.
You cannot select this check box if you have cleared the
Inherit FFT length from input dimensions check
box, and you are specifying the FFT length using the FFT
length parameter. Also, it cannot be selected when you
set the FFT implementation parameter to
FFTW.
For more information on ordering of the output, see Linear and Bit-Reversed Output Order.
Dependencies
To enable this parameter, set FFT
implementation to Auto or
Radix-2.
Input is conjugate symmetric — Input is conjugate symmetric
off (default) | on
Select this option when the block inputs conjugate symmetric data and you want real-valued outputs. Selecting this check box optimizes the block's computation method.
The FFT block yields conjugate symmetric output when you input real-valued data. Taking the IFFT of a conjugate symmetric input matrix produces real-valued output. Therefore, if the input to the block is both floating point and conjugate symmetric, and you select this check box, the block produces real-valued outputs.
You cannot select this check box if you have cleared the Inherit FFT length from input dimensions check box, and you are specifying the FFT length using the FFT length parameter.
If you input conjugate symmetric data to the IFFT block and do not select this check box, the IFFT block outputs a complex-valued signal with small imaginary parts. The block outputs invalid data if you select this option with non conjugate symmetric input data.
Divide output by FFT length — Divide output by FFT length
on (default) | off
When you select this check box, the block computes its output according to the IDFT equation, discussed in the Description section.
When you clear this check box, the block computes the output using a modified version of the IDFT: , which is defined by the following equation:
The modified IDFT equation does not include the multiplication factor of 1/M.
Inherit FFT length from input dimensions — Inherit FFT length from input dimensions
on (default) | off
Select to inherit the FFT length from the input dimensions. If you do not select this parameter, the FFT length parameter becomes available to specify the length. You cannot clear this parameter when you select either the Input is in bit-reversed order or the Input is conjugate symmetric parameter.
FFT length — FFT length
64 (default) | integer
Specify FFT length as an integer greater than or equal to two.
When you set the FFT implementation parameter to
Radix-2, or when you check the Output
in bit-reversed order check box, this value must be a
power of two.
Dependencies
To enable this parameter, clear the Inherit FFT length from input dimensions check box.
Wrap input data when FFT length is shorter than input length — Wrap or truncate the input
on (default) | off
Choose to wrap or truncate the input, depending on the FFT length. If you select this parameter, modulo-length data wrapping occurs before the FFT operation when the FFT length is shorter than the input length. If you clear this parameter, truncation of the input data to the FFT length occurs before the FFT operation.
Dependencies
To enable this parameter, clear the Inherit FFT length from input dimensions check box.
Data Types
Rounding mode — Rounding method
Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero
Select the rounding mode for fixed-point operations.
Limitations
The sine table values do not obey this parameter; instead, they
always round to Nearest.
The Rounding mode parameter has no effect on numeric results when all these conditions are met:
Product output data type is
Inherit: Inherit via internal rule.Accumulator data type is
Inherit: Inherit via internal rule.
With these data type settings, the block operates in full-precision mode.
Saturate on integer overflow — Saturate on integer overflow
off (default) | on
When you select this parameter, the block saturates the result of its
fixed-point operation. When you clear this parameter, the block wraps
the result of its fixed-point operation. For details on
saturate and wrap, see overflow
mode for fixed-point operations.
Limitations
The Saturate on integer overflow parameter has no effect on numeric results when all these conditions are met:
Product output data type is
Inherit: Inherit via internal rule.Accumulator data type is
Inherit: Inherit via internal rule.
With these data type settings, the block operates in full-precision mode.
Sine table — Data type of sine table values
Inherit: Same word length as
input (default) | fixdt(1,16)
Choose how you specify the word length of the values of the sine table. The fraction length of the sine table values always equals the word length minus one. You can set this parameter to:
A rule that inherits a data type, for example,
Inherit: Same word length as inputAn expression that evaluates to a valid data type, for example,
fixdt(1,16)
Click the Show data type assistant button ![]() to display the Data Type
Assistant, which helps you set the Sine
table parameter.
to display the Data Type
Assistant, which helps you set the Sine
table parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Limitations
The sine table values do not obey the Rounding
mode and Saturate on integer
overflow parameters; instead, they are always
saturated and rounded to Nearest.
Product output — Product output data type
Inherit: Inherit via internal
rule (default) | Inherit: Same as input | fixdt(1,16,0)
Specify the product output data type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the use of the product output data type in this block. You can set this parameter to:
A rule that inherits a data type, for example,
Inherit: Inherit via internal rule. For more information on this rule, see Inherit via Internal Rule.An expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button ![]() to display the Data Type
Assistant, which helps you set the Product
output parameter.
to display the Data Type
Assistant, which helps you set the Product
output parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Accumulator — Accumulator data type
Inherit: Inherit via internal
rule (default) | Inherit: Same as input | Inherit: Same as product output | fixdt(1,16,0)
Specify the accumulator data type. See Fixed-Point Data Types for illustrations depicting the use of the accumulator data type in this block. You can set this parameter to:
A rule that inherits a data type, for example,
Inherit: Inherit via internal rule. For more information on this rule, see Inherit via Internal Rule.An expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button ![]() to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Output — Output data type
Inherit: Inherit via internal
rule (default) | Inherit: Same as input | fixdt(1,16,0)
Specify the output data type. See Fixed-Point Data Types for illustrations depicting the use of the output data type in this block. You can set this parameter to:
A rule that inherits a data type, for example,
Inherit: Inherit via internal rule.When you select
Inherit: Inherit via internal rule, the block calculates the output word length and fraction length automatically. The equations that the block uses to calculate the ideal output word length and fraction length depend on the setting of the Divide output by FFT length check box.When you select the Divide output by FFT length check box, the ideal output word and fraction lengths are the same as the input word and fraction lengths.
When you clear the Divide output by FFT length check box, the block computes the ideal output word and fraction lengths according to the following equations:
Using these ideal results, the internal rule then selects word lengths and fraction lengths that are appropriate for your hardware. For more information, see Inherit via Internal Rule.
An expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button ![]() to display the Data Type
Assistant, which helps you set the
Output parameter.
to display the Data Type
Assistant, which helps you set the
Output parameter.
See Control Data Types of Signals (Simulink) for more information.
Output Minimum — Minimum value block should output
[] (default) | scalar
Specify the minimum value that the block should output. The default
value is [] (unspecified). Simulink software uses this value to perform:
Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types
Output Maximum — Maximum value block should output
[] (default) | scalar
Specify the maximum value that the block should output. The default
value is [] (unspecified). Simulink software uses this value to perform:
Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types
Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types
off (default) | on
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.
Block Characteristics
More About
Fixed-Point Data Types
The following diagrams show the data types used within the IFFT block for fixed-point signals. You can set the sine table, accumulator, product output, and output data types displayed in the diagrams in the IFFT block dialog box, as discussed in Parameters.
The IFFT block first casts input to the output data type and then stores it in the output buffer. Each butterfly stage then processes signals in the accumulator data type, with the final output of the butterfly being cast back into the output data type. The block multiplies in a twiddle factor before each butterfly stage in a decimation-in-time IFFT, and after each butterfly stage in a decimation-in-frequency IFFT.
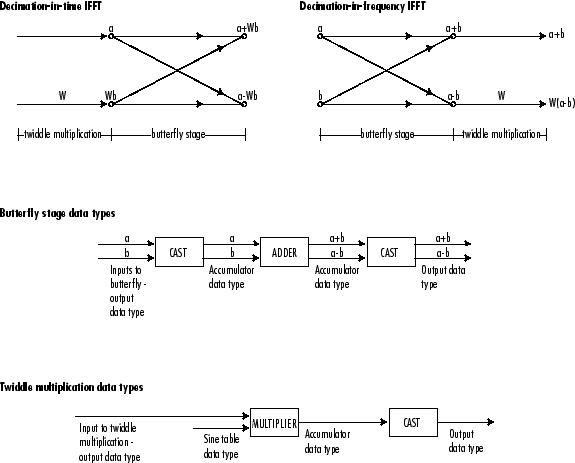
The output of the multiplier is in the accumulator data type because both of the inputs to the multiplier are complex. For details on the complex multiplication performed, see Multiplication Data Types.
Note
When the block input is fixed point, all internal data types are signed fixed point.
Algorithms
FFTW Implementation
The FFTW implementation provides an optimized FFT calculation including support for power-of-two and non-power-of-two transform lengths in both simulation and code generation. Generated code using the FFTW implementation will be restricted to MATLAB host computers. The data type must be floating-point. Refer to Simulink Coder for more details on generating code.
Radix-2 Implementation
The Radix-2 implementation supports bit-reversed processing, fixed or floating-point data, and allows the block to provide portable C-code generation using the Simulink Coder. The dimension M of the M-by-N input matrix must be a power of two. To work with other input sizes, use the Pad block to pad or truncate these dimensions to powers of two, or if possible choose the FFTW implementation.
With Radix-2 selected, the block implements one or more of the following algorithms:
Butterfly operation
Double-signal algorithm
Half-length algorithm
Radix-2 decimation-in-time (DIT) algorithm
Radix-2 decimation-in-frequency (DIF) algorithm
| Parameter Settings | Algorithms Used for IFFT Computation |
|---|---|
| Bit-reversal operation and radix-2 DIT |
| Radix-2 DIT |
| Bit-reversal operation and radix-2 DIT in conjunction with the half-length and double-signal algorithms |
| Radix-2 DIT in conjunction with the half-length and double-signal algorithms |
In certain situations, the block’s Radix–2 algorithm computes all the possible trigonometric values of the twiddle factor
where K is the greater value of either M or N and . The block stores these values in a table and retrieves them during simulation. The number of table entries for fixed-point and floating-point is summarized in the following table:
Number of Table Entries for N-Point FFT | |
|---|---|
floating-point | 3N/4 |
fixed-point | N |
References
[1] Orfanidis, S. J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1996, p. 497.
[2] Proakis, John G. and Dimitris G. Manolakis. Digital Signal Processing, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 1996.
[3] FFTW (https://www.fftw.org)
[4] Frigo, M. and S. G. Johnson, “FFTW: An Adaptive Software Architecture for the FFT,”Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vol. 3, 1998, pp. 1381-1384.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Usage notes and limitations:
When the following conditions apply, the executable generated from this block relies on prebuilt dynamic library files (
.dllfiles) included with MATLAB:FFT implementation is set to
FFTW.Inherit FFT length from input dimensions is cleared, and FFT length is set to a value that is not a power of two.
Use the
packNGofunction to package the code generated from this block and all the relevant files in a compressed zip file. Using this zip file, you can relocate, unpack, and rebuild your project in another development environment where MATLAB is not installed. For more details, see How To Run a Generated Executable Outside MATLAB.When the FFT length is a power of two, you can generate standalone C and C++ code from this block.
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)