Good Vibrations
By Cleve Moler, MathWorks
eigshow helps explain eigenvalues and singular values
Many of the world's most interesting phenomena—vibration, resonance, stability, quantum energy levels, even our L-shaped membrane—involve eigenvalues and eigenvectors. The word eigenvalue comes from the German word eigenwert. Like liverwurst, only half of it has been translated. Some older textbooks tried more complete translations like characteristic value or proper value, but these never caught on. A related concept is singular value. This is also an unusual term because it has almost nothing to do with singularity.
During the recent MATLAB Conferences, we presented a new example—eigshow—which helps explain and compare eigenvalues and singular values. The plots in this article are snapshots of the display produced by eigshow, but you really have to see it in action to get its full impact. It will be included in MATLAB 5.2.
We can illustrate how eigshow works with the matrix
\[A = \begin{bmatrix}\frac{1}{4} & \frac{3}{4} \\ 1 & \frac{1}{2}\end{bmatrix}\]
Initially, eigshow plots the unit vector \(x = [1, 0]^{\mathrm{T}}\), as well as the vector \(Ax\), which starts out as the first column of \(A\). You can then use your mouse to move \(x\), shown in green, around the unit circle. As you move \(x\), the resulting \(Ax\), shown in blue, also moves. The first four plots show intermediate steps as \(x\) traces out a green unit circle. What is the shape of the resulting orbit of \(Ax\)? An important, and nontrivial, theorem from linear algebra tells us that the blue curve is an ellipse. eigshow provides a "proof by GUI" of this theorem.

The figure caption says "Make \(Ax\) parallel to \(x\)." If \(A\) is any matrix (or linear operator) then an eigenvalue of \(A\) is a scalar IMAGE for which the equation
\[Ax = \lambda x\]
has a nonzero solution, \(x\), the corresponding eigenvector (or eigenfunction). This says that, in the direction \(x\), the operator \(A\) is simply a stretching or magnification by the value \(\lambda\). In various mathematical models, the values of \(\lambda\) correspond to frequencies of vibration, or critical values of stability parameters, or energy levels of atoms.
The next two plots show the eigenvalues and eigenvectors of our 2-by-2 example. The first eigenvalue is positive, so \(Ax\) lies on top of the eigenvector \(x\). The length of \(Ax\) is the corresponding eigenvalue; it happens to be 5/4 in this example. The second eigenvalue is negative, so \(Ax\) is parallel to \(x\), but points in the opposite direction. The length of \(Ax\) is 1/2, and the corresponding eigenvalue is actually -1/2.
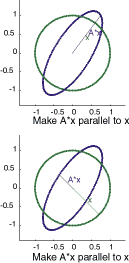
You might have noticed that the two eigenvectors are not the major and minor axes of the ellipse. They would be if the matrix were symmetric. This matrix is close to, but not exactly equal to, a symmetric matrix. For other matrices, it may not be possible to find a real \(x\) so that \(Ax\) is parallel to \(x\). These examples, which we don't have room to show here, demonstrate that 2-by-2 matrices can have fewer than two real eigenvectors.
The axes of the ellipse do play a key role in the singular value decomposition. The results produced by the "svd" mode of eigshow are shown in the final plot. Again, the mouse moves \(x\) around the unit circle, but now a second unit vector, \(y\), follows \(x\), staying perpendicular to it. The resulting \(Ax\) and \(Ay\) traverse the ellipse, but are not usually perpendicular to each other. The goal is to make them perpendicular. When they are, they form the axes of the ellipse. The vectors \(x\) and \(y\) are the right singular vectors of \(A\), the vectors \(Ax\) and \(Ay\) are multiples of the left singular vectors, and the lengths of the axes are the singular values.
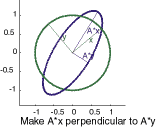
If a matrix is square, symmetric, and positive definite, then its eigenvalue decomposition and singular value decomposition are the same.
In abstract linear algebra terms, eigenvalues are relevant when a square, n-by-n matrix \(A\) is thought of as mapping n-dimensional space onto itself. This is the situation, for example, in the analysis of systems of ordinary differential equations. We try to find a basis for the space so that the matrix becomes diagonal. This basis might be complex, even when \(A\) is real. In fact, if the Jordan canonical form is not diagonal, such a basis does not even exist.
The singular value decomposition is relevant when a possibly rectangular, m-by-n matrix \(A\) is thought of as mapping n-space onto m-space. This is the situation in the analysis of systems of simultaneous linear equations. We try to find one change of basis in the domain and a usually different change of basis in the range so that the matrix becomes diagonal. Such bases always exist and are always real when \(A\) is real. In fact, the transforming matrices are orthogonal, so they preserve lengths and angles and do not magnify errors.
We hope that eigshow will help explain the wonders of eigenvalues and singular values.
Published 1998