Loop Shape and Stability Margin Specifications
This example shows how to specify loop shapes and stability margins when tuning control systems with systune or looptune.
The systune and looptune functions tune the parameters of fixed-structure control systems subject to a variety of time- and frequency-domain requirements. To specify these design requirements, use tuning goal objects.
Loop Shape
The TuningGoal.LoopShape requirement is used to shape the open-loop response gain(s), a design approach known as loop shaping. For example,
s = tf('s'); R1 = TuningGoal.LoopShape('u',1/s);
specifies that the open-loop response measured at the location "u" should look like a pure integrator (as far as its gain is concerned). In MATLAB®, use an AnalysisPoint block to mark the location "u", see the "Building Tunable Models" example for details. In Simulink®, use the addPoint method of the slTuner interface to mark "u" as a point of interest.
As with other gain specifications, you can just specify the asymptotes of the desired loop shape using a few frequency points. For example, to specify a loop shape with gain crossover at 1 rad/s, -20 dB/decade slope before 1 rad/s, and -40 dB/decade slope after 1 rad/s, just specify that the gain at the frequencies 0.1,1,10 should be 10,1,0.01, respectively.
LS = frd([10,1,0.01],[0.1,1,10]); R2 = TuningGoal.LoopShape('u',LS); bodemag(LS,R2.LoopGain) legend('Specified','Interpolated')
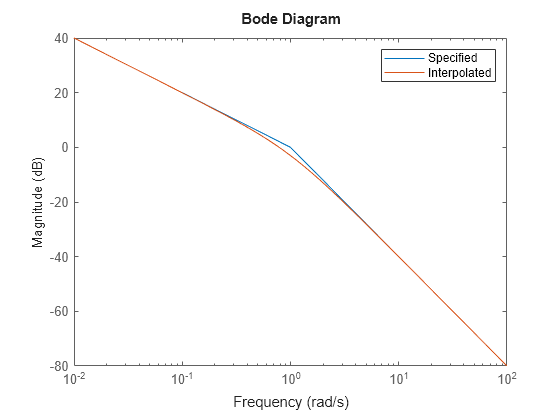
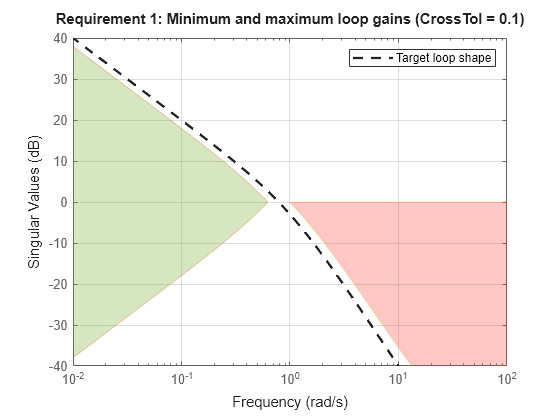
Loop shape requirements are constraints on the open-loop response . For tuning purposes, they are converted into closed-loop gain constraints on the sensitivity function and complementary sensitivity function . Use viewGoal to visualize the target loop shape and corresponding gain bounds on (green) and (red).
viewGoal(R2)
Minimum and Maximum Loop Gain
Instead of TuningGoal.LoopShape, you can use TuningGoal.MinLoopGain and TuningGoal.MaxLoopGain to specify minimum or maximum values for the loop gain in a particular frequency band. This is useful when the actual loop shape near crossover is best left to the tuning algorithm to figure out. For example, the following requirements specify the minimum loop gain inside the bandwidth and the roll-off characteristics outside the bandwidth, but do not specify the actual crossover frequency nor the loop shape near crossover.
MinLG = TuningGoal.MinLoopGain('u',5/s); % integral action MinLG.Focus = [0 0.2]; MaxLG = TuningGoal.MaxLoopGain('u',1/s^2); % -40dB/decade roll off MaxLG.Focus = [1 Inf]; viewGoal([MinLG MaxLG])

The TuningGoal.MaxLoopGain requirement rests on the fact that the open- and closed-loop gains are comparable when the loop gain is small (). As a result, it can be ineffective at keeping the loop gain below some value close to 1. For example, suppose that flexible modes cause gain spikes beyond the crossover frequency and that you need to keep these spikes below 0.5 (-6 dB). Instead of using TuningGoal.MaxLoopGain, you can directly constrain the gain of using TuningGoal.Gain with a loop opening at "u".
MaxLG = TuningGoal.Gain('u','u',0.5); MaxLG.Opening = 'u';
If the open-loop response is unstable, make sure to further disable the implicit stability constraint associated with this requirement.
MaxLG.Stabilize = false;
Figure 1 shows this requirement evaluated for an open-loop response with flexible modes.

Figure 1: Gain constraint on L
Stability Margins
The TuningGoal.Margins requirement uses the notion of disk margin to enforce minimum amounts of gain and phase margins at the specified loop opening site(s). For MIMO feedback loops, this requirement guarantees stability for gain or phase variations in each feedback channel. The gain or phase can change in all channels simultaneously, and by a different amount in each channel. See Stability Margins in Control System Tuning for details. For example,the following code enforces dB of gain margin and 45 degrees of phase margin at a location "u".
R = TuningGoal.Margins('u',6,45);In MATLAB, use an AnalysisPoint block to mark the location "u" (see Building Tunable Models for details). In Simulink, use the addPoint method of the slTuner interface to mark "u" as a point of interest (see Create and Configure slTuner Interface to Simulink Model (Simulink Control Design)). Stability margins are typically measured at the plant inputs or plant outputs or both.
The target gain and phase margin values are converted into a normalized gain constraint on some appropriate closed-loop transfer function. The desired margins are achieved at frequencies where the gain is less than 1. Use viewGoal to examine the requirement you have configured.
viewGoal(R)

The shaded region indicates where the constraint is violated. After tuning, for a tuned model T, you can use viewGoal(R,T) to see the tuned frequency-dependent margins on this plot.
See Also
TuningGoal.MinLoopGain | TuningGoal.MaxLoopGain | TuningGoal.LoopShape | TuningGoal.Margins