Bond Prices and Yield Curve Parallel Shifts
This example uses Financial Toolbox™ bond pricing functions to evaluate the impact of time-to-maturity and yield variation on the price of a bond portfolio. Also, this example shows how to visualize the price behavior of a portfolio of bonds over a wide range of yield curve scenarios, and as time progresses toward maturity.
Specify values for the settlement date, maturity date, face value, coupon rate, and coupon payment periodicity of a four-bond portfolio. For simplicity, accept default values for the end-of-month payment rule (rule in effect) and day-count basis (actual/actual). Also, synchronize the coupon payment structure to the maturity date (no odd first or last coupon dates). Any inputs for which defaults are accepted are set to empty matrices ([]) as placeholders where appropriate. Also, specify the points on the yield curve for each bond.
Settle = datetime(1995,1,15); Maturity = datetime( [2020, 4, 3;... 2025, 5,14;... 2019, 6, 9;... 2019, 2,25])
Maturity = 4×1 datetime
03-Apr-2020
14-May-2025
09-Jun-2019
25-Feb-2019
Face = [1000; 1000; 1000; 1000]; CouponRate = [0; 0.05; 0; 0.055]; Periods = [0; 2; 0; 2]; Yields = [0.078; 0.09; 0.075; 0.085];
Use Financial Toolbox functions to calculate the true bond prices as the sum of the quoted price plus accrued interest.
[CleanPrice, AccruedInterest] = bndprice(Yields,... CouponRate,Settle, Maturity, Periods,... [], [], [], [], [], [], Face); Prices = CleanPrice + AccruedInterest
Prices = 4×1
145.2452
594.7757
165.8949
715.7584
Assume that the value of each bond is $25,000, and determine the quantity of each bond such that the portfolio value is $100,000.
BondAmounts = 25000 ./ Prices;
Compute the portfolio price for a rolling series of settlement dates over a range of yields. The evaluation dates occur annually on January 15, beginning on 15-Jan-1995 (settlement) and extending out to 15-Jan-2018. Thus, this step evaluates portfolio price on a grid of time of progression (dT) and interest rates (dY).
dy = -0.05:0.005:0.05; % Yield changes D = datevec(Settle); % Get date components dt = datetime(year(Settle):2018, month(Settle), day(Settle)); % Get evaluation dates [dT, dY] = meshgrid(dt, dy); % Create grid NumTimes = length(dt); % Number of time steps NumYields = length(dy); % Number of yield changes NumBonds = length(Maturity); % Number of bonds % Preallocate vector Prices = zeros(NumTimes*NumYields, NumBonds);
Now that the grid and price vectors have been created, compute the price of each bond in the portfolio on the grid one bond at a time.
for i = 1:NumBonds [CleanPrice, AccruedInterest] = bndprice(Yields(i)+... dY(:), CouponRate(i), dT(:), Maturity(i), Periods(i),... [], [], [], [], [], [], Face(i)); Prices(:,i) = CleanPrice + AccruedInterest; end
Scale the bond prices by the quantity of bonds and reshape the bond values to conform to the underlying evaluation grid.
Prices = Prices * BondAmounts; Prices = reshape(Prices, NumYields, NumTimes);
Plot the price of the portfolio as a function of settlement date and a range of yields, and as a function of the change in yield (dY). This plot illustrates the interest-rate sensitivity of the portfolio as time progresses (dT), under a range of interest-rate scenarios. With the following graphics commands, you can visualize the three-dimensional surface relative to the current portfolio value (that is, $100,000).
figure % Open a new figure window surf(dt, dy, Prices) % Draw the surface hold on % Add the current value for reference basemesh = mesh(dt, dy, 100000*ones(NumYields, NumTimes)); set(basemesh, 'facecolor', 'none'); set(basemesh, 'edgecolor', 'm'); set(gca, 'box', 'on'); xlim(datetime([1993,2020],1,1)) xlabel('Evaluation Date'); ylabel('Change in Yield'); zlabel('Portfolio Price'); hold off view(-25,25);
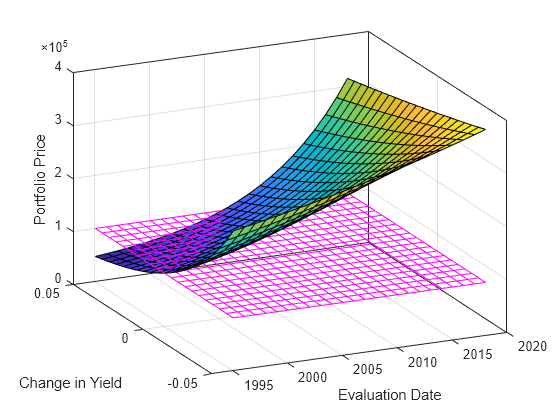
MATLAB® three-dimensional graphics allow you to visualize the interest-rate risk experienced by a bond portfolio over time. This example assumed parallel shifts in the term structure, but it might similarly have allowed other components to vary, such as the level and slope.
See Also
bnddury | bndconvy | bndprice | bndkrdur | blsprice | blsdelta | blsgamma | blsvega | zbtprice | zero2fwd | zero2disc
Topics
- Pricing and Analyzing Equity Derivatives
- Greek-Neutral Portfolios of European Stock Options
- Sensitivity of Bond Prices to Interest Rates
- Bond Portfolio for Hedging Duration and Convexity
- Bond Prices and Yield Curve Nonparallel Shifts
- Term Structure Analysis and Interest-Rate Swaps
- Plotting Sensitivities of an Option
- Plotting Sensitivities of a Portfolio of Options