Main Content

Fixed-Point Function Approximation

Open Live Script

When a fixed-point library function is not available, fixed-point applications require an approximation of the function. Often, an interpolated look up table is used to store an approximation of the function over a specified range.

This example shows how to approximate the function y = sin(2*pi*x) over a specified input range using a lookup table.

In this example, the input uses an unsigned 16-bit data type, fixdt(0,16,16), and the output uses a signed 16-bit data type, fixdt(1,16,14).

The goal of this example is to create an approximation that is accurate to 8 bits to the right of the binary point. This means that the worst case error should be less than 2^(-8).

There are many sets of lookup table data points that would meet this goal. Different implementations can be chosen depending on goals such as memory usage and speed of computation. This example finds a solution that meets this accuracy goal with the minimal number of data points.

Approximate Function

Use the FunctionApproximation.Options object to specify accuracy and word length constraints.

options = FunctionApproximation.Options();
options.AbsTol = 2^-8;
options.RelTol = 0;
options.WordLengths = [8 16 32];
options.MemoryUnits = 'bytes';
options.OnCurveTableValues = true;

Specify the function to approximate and the input ranges and data types in the FunctionApproximation.Problem object.

functionToApproximate = @(x) sin(2*pi*x);

problem = FunctionApproximation.Problem(functionToApproximate, 'Options', options);
problem.InputTypes = numerictype(0,16,16);
problem.InputLowerBounds = 0;
problem.InputUpperBounds = 0.25;
problem.OutputType = numerictype(1,16,14);

Create a lookup table solution.

solution = solve(problem);
Searching for fixed-point solutions.

|  ID | Memory (bytes) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification |             Error(Max,Current) | 
|   0 |     4.0000e+00 |        0 |          2 |               8 |            8 |             EvenSpacing |     3.906250e-03, 2.105137e-01 |
|   1 |     1.9000e+01 |        0 |         17 |               8 |            8 |             EvenSpacing |     3.906250e-03, 4.257483e-03 |
|   2 |     3.5000e+01 |        1 |         33 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.848536e-03 |
|   3 |     2.8000e+01 |        1 |         26 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.768435e-03 |
|   4 |     2.4000e+01 |        1 |         22 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.596819e-03 |
|   5 |     2.1000e+01 |        1 |         19 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.589720e-03 |
|   6 |     1.5000e+01 |        0 |         13 |               8 |            8 |             EvenSpacing |     3.906250e-03, 7.812500e-03 |
|   7 |     1.7000e+01 |        1 |         15 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.824648e-03 |
|   8 |     1.2000e+01 |        0 |         10 |               8 |            8 |             EvenSpacing |     3.906250e-03, 4.677033e-03 |
|   9 |     1.1000e+01 |        0 |          9 |               8 |            8 |             EvenSpacing |     3.906250e-03, 6.957420e-03 |
|  10 |     1.4000e+01 |        1 |         12 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.687388e-03 |
|  11 |     1.3000e+01 |        0 |         11 |               8 |            8 |             EvenSpacing |     3.906250e-03, 7.812500e-03 |
|  12 |     9.0000e+00 |        0 |          7 |               8 |            8 |             EvenSpacing |     3.906250e-03, 7.818172e-03 |
|  13 |     6.0000e+00 |        0 |          2 |              16 |            8 |             EvenSpacing |     3.906250e-03, 2.105137e-01 |
|  14 |     1.3000e+01 |        0 |          9 |              16 |            8 |             EvenSpacing |     3.906250e-03, 6.957420e-03 |
|  15 |     6.0000e+00 |        0 |          2 |               8 |           16 |             EvenSpacing |     3.906250e-03, 2.105137e-01 |
|  16 |     4.0000e+00 |        0 |          2 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|  17 |     1.1000e+01 |        0 |          9 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 6.957420e-03 |
|  18 |     6.0000e+00 |        0 |          2 |              16 |            8 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|  19 |     1.3000e+01 |        0 |          9 |              16 |            8 |         EvenPow2Spacing |     3.906250e-03, 6.957420e-03 |
|  20 |     6.0000e+00 |        0 |          2 |               8 |           16 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|  21 |     8.0000e+00 |        0 |          2 |              16 |           16 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|  22 |     1.4000e+01 |        1 |          7 |               8 |            8 |          ExplicitValues |     3.906250e-03, 3.830054e-03 |
|  23 |     3.5000e+01 |        1 |         33 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 3.848536e-03 |

Best Solution
|  ID | Memory (bytes) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification |             Error(Max,Current) |
|  10 |     1.4000e+01 |        1 |         12 |               8 |            8 |             EvenSpacing |     3.906250e-03, 3.687388e-03 |

Change breakpoint specification to EvenPow2Spacing and create a lookup table solution again

problem.Options.BreakpointSpecification = 'EvenPow2Spacing';
bestEvenPow2SpacingSolution = solve(problem);
Searching for fixed-point solutions.

|  ID | Memory (bytes) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification |             Error(Max,Current) | 
|   0 |     4.0000e+00 |        0 |          2 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|   1 |     1.9000e+01 |        0 |         17 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 4.257483e-03 |
|   2 |     3.5000e+01 |        1 |         33 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 3.848536e-03 |
|   3 |     1.1000e+01 |        0 |          9 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 6.957420e-03 |
|   4 |     6.0000e+00 |        0 |          2 |              16 |            8 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|   5 |     2.1000e+01 |        0 |         17 |              16 |            8 |         EvenPow2Spacing |     3.906250e-03, 4.257483e-03 |
|   6 |     1.3000e+01 |        0 |          9 |              16 |            8 |         EvenPow2Spacing |     3.906250e-03, 6.957420e-03 |
|   7 |     6.0000e+00 |        0 |          2 |               8 |           16 |         EvenPow2Spacing |     3.906250e-03, 2.105137e-01 |
|   8 |     2.0000e+01 |        0 |          9 |               8 |           16 |         EvenPow2Spacing |     3.906250e-03, 4.856432e-03 |

Best Solution
|  ID | Memory (bytes) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification |             Error(Max,Current) |
|   2 |     3.5000e+01 |        1 |         33 |               8 |            8 |         EvenPow2Spacing |     3.906250e-03, 3.848536e-03 |

Explore Solutions

The software returns several implementations that meet the requirements specified in the FunctionApproximation.Problem and FunctionApproximation.Options objects. You can explore these different implementations.

feasibleSolutions = solution.FeasibleSolutions;
tableDataVec = [feasibleSolutions.TableData];
evenSpacingSolutions = find([tableDataVec.IsEvenSpacing]);
unevenSpacingSolutions = find(~[tableDataVec.IsEvenSpacing]);

evenSolutionsMemoryUsage   = arrayfun(@(x) x.totalMemoryUsage(), feasibleSolutions(evenSpacingSolutions));
unevenSolutionsMemoryUsage = arrayfun(@(x) x.totalMemoryUsage(), feasibleSolutions(unevenSpacingSolutions));

bestEvenSpacingSolution  = feasibleSolutions(evenSpacingSolutions(evenSolutionsMemoryUsage == min(evenSolutionsMemoryUsage)));
bestUnevenSpacingSolution = feasibleSolutions(unevenSpacingSolutions(unevenSolutionsMemoryUsage == min(unevenSolutionsMemoryUsage)));

xeven = bestEvenSpacingSolution.TableData.BreakpointValues{1};
yeven = bestEvenSpacingSolution.TableData.TableValues;

xuneven = bestUnevenSpacingSolution.TableData.BreakpointValues{1};
yuneven = bestUnevenSpacingSolution.TableData.TableValues;

xpow2 = bestEvenPow2SpacingSolution.TableData.BreakpointValues{1};
ypow2 = bestEvenPow2SpacingSolution.TableData.TableValues;

Compare Memory Usage

Compare the memory used by the lookup tables.

memoryValues = [...
    totalMemoryUsage(bestEvenPow2SpacingSolution), ...
    totalMemoryUsage(bestEvenSpacingSolution), ...
    totalMemoryUsage(bestUnevenSpacingSolution)];

figure();
xTickLabels = {'Even pow2 spacing \newline(fastest)','Even spacing \newline(faster)','Uneven spacing \newline(fast)'};
hMemory = bar(memoryValues);
title('Comparison of memory usage obtained by different \newline breakpoint specification options');
hMemory.Parent.XTickLabel = xTickLabels;
hMemory.Parent.XTickLabelRotation = 45;
hMemory.Parent.YLabel.String = 'Memory (bytes)';
hMemory.Parent.Box = 'on';
hMemory.Parent.YGrid = 'on';

Figure contains an axes object. The axes object with title Comparison of memory usage obtained by different Start 2 by 1 matrix 1st Row 1st Column undefined 2nd Row 1st Column undefined EndMatrix breakpoint specification options, ylabel Memory (bytes) contains an object of type bar.

The amount of memory used by the tables using even spacing and uneven spacing are the same, but the number of points are different. This is because when storing the breakpoints for tables using even spacing, only the first point and spacing are stored. In contrast, all breakpoints are stored for tables using uneven spacing.

EvenPow2Spacing stores more than double the points stored for even spacing. From a memory usage perspective, EvenPow2Spacing is the least optimal for this function. However, computations for EvenPow2Spacing are performed using arithmetic shifts instead of multiplication, which can lead to faster execution times.

Compare Solutions to Original Function

Compare the solution using EvenPow2Spacing to the original function.

[~, hEvenPow2Spacing] = compare(bestEvenPow2SpacingSolution);
hEvenPow2Spacing.Children(4).Title.String = [hEvenPow2Spacing.Children(4).Title.String ' (Even pow2 spacing)'];

Figure contains 2 axes objects. Axes object 1 with title Comparison of Original Function and Approximation (Even pow2 spacing), xlabel Input, ylabel Function Value contains 2 objects of type line. These objects represent Original, Approximation. Axes object 2 with title Feasibility of Solution: Feasible AbsTol = 0.00390625 RelTol = 0, xlabel Input, ylabel Error contains 3 objects of type area, line. These objects represent Feasible Region : Absolute Error <= Max Error Allowed, Max Error Allowed : max(abs(Original) * RelTol, AbsTol), Absolute Error : abs(Original - Approximation).

Compare the solution using even spacing to the original function.

[~, hEvenSpacing] = compare(bestEvenSpacingSolution);
hEvenSpacing.Children(4).Title.String = [hEvenSpacing.Children(4).Title.String ' (Even spacing)'];

Figure contains 2 axes objects. Axes object 1 with title Comparison of Original Function and Approximation (Even spacing), xlabel Input, ylabel Function Value contains 2 objects of type line. These objects represent Original, Approximation. Axes object 2 with title Feasibility of Solution: Feasible AbsTol = 0.00390625 RelTol = 0, xlabel Input, ylabel Error contains 3 objects of type area, line. These objects represent Feasible Region : Absolute Error <= Max Error Allowed, Max Error Allowed : max(abs(Original) * RelTol, AbsTol), Absolute Error : abs(Original - Approximation).

Compare the solution using uneven spacing to the original function.

[~, hUnevenSpacing] = compare(bestUnevenSpacingSolution);
hUnevenSpacing.Children(4).Title.String = [hUnevenSpacing.Children(4).Title.String ' (Uneven spacing)'];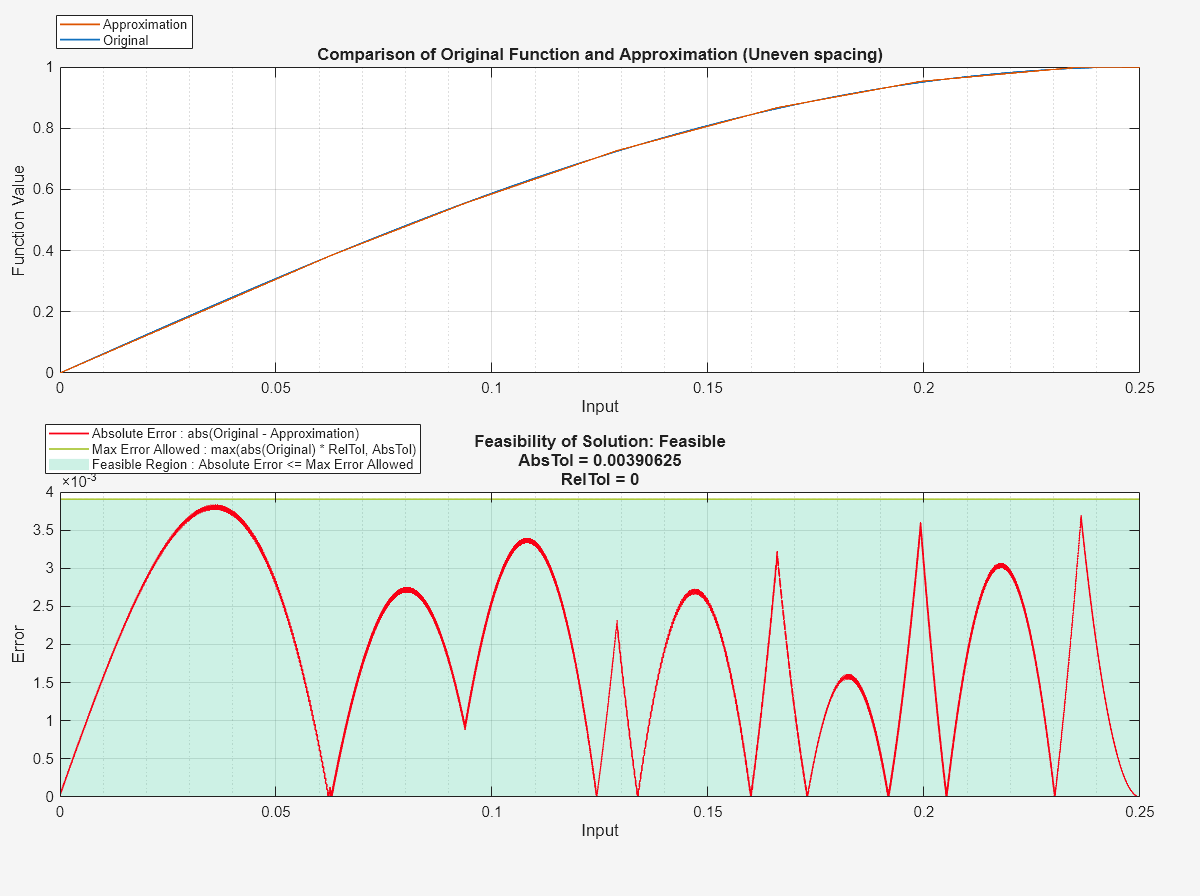

Figure contains 2 axes objects. Axes object 1 with title Comparison of Original Function and Approximation (Uneven spacing), xlabel Input, ylabel Function Value contains 2 objects of type line. These objects represent Original, Approximation. Axes object 2 with title Feasibility of Solution: Feasible AbsTol = 0.00390625 RelTol = 0, xlabel Input, ylabel Error contains 3 objects of type area, line. These objects represent Feasible Region : Absolute Error <= Max Error Allowed, Max Error Allowed : max(abs(Original) * RelTol, AbsTol), Absolute Error : abs(Original - Approximation).

Use Approximation in Simulink Model

You can use this approximation directly in a Simulink Lookup Table (n-D) block. The fxpdemo_approx model compares the lookup tables with different breakpoint spacing specification. The LUTs approximate the function sin(2*pi*x).

modelName = 'fxpdemo_approx';
open_system(modelName)

modelWorkspace = get_param(modelName, 'ModelWorkspace');

modelWorkspace.assignin('xevenFirstPoint'     , xeven(1)  );
modelWorkspace.assignin('xevenSpacing'        , diff(xeven(1:2))  );
modelWorkspace.assignin('yeven'               , yeven  );
modelWorkspace.assignin('TableDTeven'         , bestEvenSpacingSolution.TableData.TableDataType      );
modelWorkspace.assignin('BreakpointDTeven'    , bestEvenSpacingSolution.TableData.BreakpointDataTypes);

modelWorkspace.assignin('xuneven'             , xuneven);
modelWorkspace.assignin('yuneven'             , yuneven);
modelWorkspace.assignin('TableDTuneven'       , bestUnevenSpacingSolution.TableData.TableDataType      );
modelWorkspace.assignin('BreakpointDTuneven'  , bestUnevenSpacingSolution.TableData.BreakpointDataTypes);

modelWorkspace.assignin('xpow2FirstPoint'     , xpow2(1)  );
modelWorkspace.assignin('xpow2Spacing'        , diff(xpow2(1:2))  );
modelWorkspace.assignin('ypow2'               , ypow2  );
modelWorkspace.assignin('TableDTpow2'         , bestEvenPow2SpacingSolution.TableData.TableDataType      );
modelWorkspace.assignin('BreakpointDTpow2'    , bestEvenPow2SpacingSolution.TableData.BreakpointDataTypes);

set_param(modelName, 'Dirty', 'off');

Summary

The ideal function and the three approximations are used in the model fxpdemo_approx. Simulate the model.

sim(modelName)

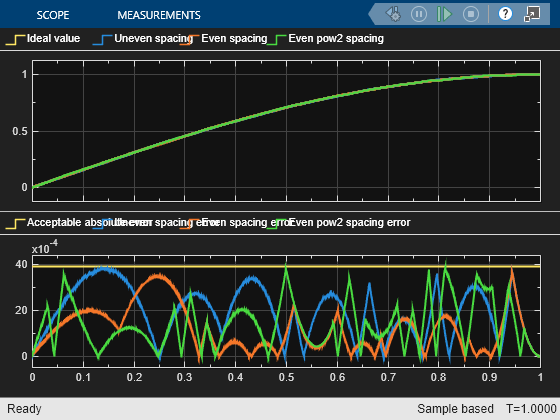
Generate Code

If you have Simulink® Coder™ installed, you can generate code for the model. If inline parameters is ON, the generated code will show the large efficiency differences in the implementation of unevenly spaced, evenly spaced, and power of 2 spacing.