Design Model Predictive Controller at Equilibrium Operating Point
This example shows how to design a model predictive controller with nonzero nominal values.
The plant model is obtained by linearization of a nonlinear plant in Simulink® at a nonzero steady-state operating point.
Linearize Nonlinear Plant Model
The nonlinear plant is implemented in the Simulink model mpc_nloffsets and linearized at the default operating condition using the linearize function from Simulink Control Design™.
Create an operating point specification for the current model initial conditions.
plant_mdl = 'mpc_nloffsets';
op = operspec(plant_mdl);
Compute the operating point for these initial conditions.
[op_point, op_report] = findop(plant_mdl,op);
Operating point search report:
---------------------------------
opreport =
Operating point search report for the Model mpc_nloffsets.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) mpc_nloffsets/Integrator
-Inf 0.57514 Inf 0 -1.8208e-14 0
(2.) mpc_nloffsets/Integrator2
-Inf 2.1503 Inf 0 -8.3846e-12 0
Inputs:
----------
Min u Max
______ ______ ______
(1.) mpc_nloffsets/In1
-Inf -1.252 Inf
Outputs:
----------
Min y Max
________ ________ ________
(1.) mpc_nloffsets/Out1
-Inf -0.52938 Inf
Extract nominal state, output, and input values from the computed operating point.
x0 = [op_report.States(1).x;op_report.States(2).x]; y0 = op_report.Outputs.y; u0 = op_report.Inputs.u;
Linearize the plant at the initial conditions.
plant = linearize(plant_mdl,op_point);
Design MPC Controller
Create an MPC controller object with a specified sample time Ts, prediction horizon 20, and control horizon 3.
Ts = 0.1; mpcobj = mpc(plant,Ts,20,3);
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
Set the nominal values in the controller.
mpcobj.Model.Nominal = struct('X',x0,'U',u0,'Y',y0);
Set the output measurement noise model (white noise, zero mean, standard deviation = 0.1).
mpcobj.Model.Noise = 0.1;
Set the manipulated variable constraint.
mpcobj.MV.Max = 0.2;
Simulate Using Simulink
Specify the reference value for the output signal.
r0 = 1.5*y0;
Open and simulate the model.
mdl = 'mpc_offsets';
open_system(mdl)
sim(mdl)
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise.



Simulate Using sim Command
Simulate the controller.
Tf = round(10/Ts); r = r0*ones(Tf,1); [y1,t1,u1,x1,xmpc1] = sim(mpcobj,Tf,r);
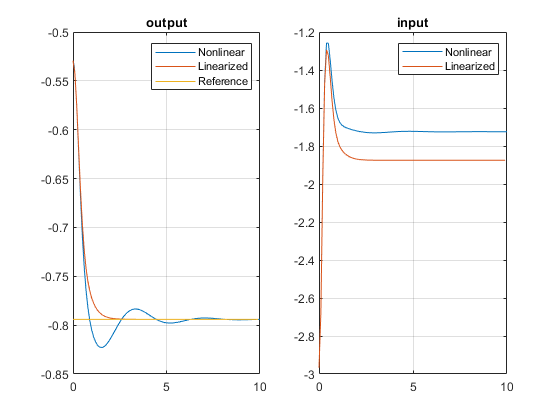
Plot and compare the simulation results.
subplot(1,2,1) plot(y.time,y.signals.values,t1,y1,t1,r) legend('Nonlinear','Linearized','Reference') title('output') grid subplot(1,2,2) plot(u.time,u.signals.values,t1,u1) legend('Nonlinear','Linearized') title('input') grid
bdclose(plant_mdl) bdclose(mdl)