Setting Targets for Manipulated Variables
When there are more manipulated variables than outputs, assuming that the static gain matrix is full rank, it is possible for the controller to reach any given steady state point in the output space using many different possible combinations of manipulated variable values.
In this case, for economic or operational reasons, you can choose to set target values, and some corresponding nonzero cost function weights, for some manipulated variables (up to the excess number of manipulated variables with respect to the number of outputs). The remaining manipulated variables can attain the values required to track any point in the steady-state output space.
This example shows how to design a model predictive controller for a plant with two inputs and one output with target setpoint for one of the two manipulated variables.
Define Plant Model
The linear plant model has two inputs and one output. Define the plant as a transfer function, convert it to state space, specify the initial state, and extract the plant matrices for later use within the Simulink® model.
plant = ss(tf({[3 1],[2 1]},{[1 2*.3 1],[1 2*.5 1]}));
x0 = [0 0 0 0]';
A = plant.A;
B = plant.B;
C = plant.C;
D = plant.D;
Design MPC Controller
Create an MPC controller with sampling time 0.4 s, and prediction and control horizons of 20 and 5 steps, respectively.
mpcobj = mpc(plant,0.4,20,5);
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
Specify weights for both manipulated variables and output.
mpcobj.weights.manipulated = [0.3 0]; % weight difference MV#1 - Target#1
mpcobj.weights.manipulatedrate = [0 0];
mpcobj.weights.output = 1;
Define constraints for the manipulated variable rate.
mpcobj.MV = struct('RateMin',{-0.5;-0.5},'RateMax',{0.5;0.5});
Set Target for One Manipulated Variable
Specify target setpoint u = 2 for the first manipulated variable.
mpcobj.MV(1).Target=2;
Simulate with Simulink
Define the model name and open the Simulink model. Note that the output reference is a square wave. Then simulate the model, using the sim command.
mdl = 'mpc_utarget';
open_system(mdl)
sim(mdl);
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output.


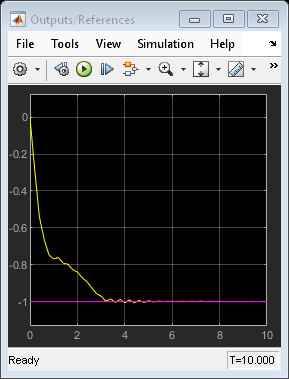
The first plot shows that the first manipulated variable reaches its set point after about 6 seconds, while the plant output reaches its reference.
bdclose(mdl) % close the Simulink model