patternAzimuth
System object: phased.HeterogeneousConformalArray
Namespace: phased
Plot heterogeneous conformal array directivity or pattern versus azimuth
Syntax
patternAzimuth(sArray,FREQ)
patternAzimuth(sArray,FREQ,EL)
patternAzimuth(sArray,FREQ,EL,Name,Value)
PAT = patternAzimuth(___)
Description
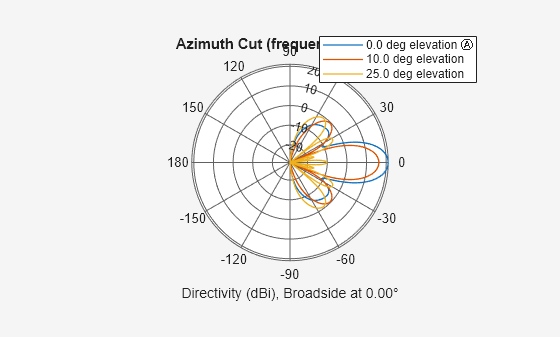
patternAzimuth( plots
the 2-D array directivity pattern versus azimuth (in dBi) for the
array sArray,FREQ)sArray at zero degrees elevation angle.
The argument FREQ specifies the operating frequency.
The integration used when computing array directivity has a minimum sampling grid of 0.1 degrees. If an array pattern has a beamwidth smaller than this, the directivity value will be inaccurate.
patternAzimuth(,
in addition, plots the 2-D array directivity pattern versus azimuth (in dBi) for the array
sArray,FREQ,EL)sArray at the elevation angle specified by EL.
When EL is a vector, multiple overlaid plots are created.
patternAzimuth(
plots the array pattern with additional options specified by one or
more sArray,FREQ,EL,Name,Value)Name,Value pair arguments.
PAT = patternAzimuth(___)PAT is a matrix whose entries
represent the pattern at corresponding sampling points specified by
the 'Azimuth' parameter and the EL input
argument.
Input Arguments
Name-Value Arguments
Output Arguments
Examples
More About
Version History
Introduced in R2015a