Local Restriction (G)
Restriction in flow area in gas network
Libraries:
Simscape /
Foundation Library /
Gas /
Elements
Description
The Local Restriction (G) block models the pressure drop due to a localized reduction in flow area, such as a valve or an orifice, in a gas network. Choking occurs when the restriction reaches the sonic condition.
Ports A and B represent the restriction inlet and outlet. The input physical signal at port AR specifies the restriction area. Alternatively, you can specify a fixed restriction area as a block parameter.
The block icon changes depending on the value of the Restriction type parameter.
| Restriction Type | Block Icon |
|---|---|
|
|
|
|
The restriction is adiabatic. It does not exchange heat with the environment.
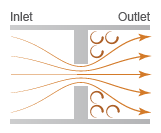
The restriction consists of a contraction followed by a sudden expansion in flow area. The gas accelerates during the contraction, causing the pressure to drop. The gas separates from the wall during the sudden expansion, causing the pressure to recover only partially due to the loss of momentum.
Local Restriction Schematic
Caution
Gas flow through this block can choke. If a Mass Flow Rate Source (G) block or a Controlled Mass Flow Rate Source (G) block connected to the Local Restriction (G) block specifies a greater mass flow rate than the possible choked mass flow rate, the simulation generates an error. For more information, see Choked Flow.
Mass Balance
The mass balance equation is:
where A and B are the mass flow rates at ports A and B, respectively. Flow rate associated with a port is positive when it flows into the block.
Energy Balance
The energy balance equation is:
where ΦA and ΦB are energy flow rates at ports A and B, respectively.
The block is assumed adiabatic. Therefore, there is no change in specific total enthalpy between port A, port B, and the restriction:
where h is the specific enthalpy at port A, port B, or restriction R, as indicated by the subscript.
The ideal flow velocities at port A, port B, and the restriction are:
where:
S is the cross-sectional area at ports A and B.
SR is the cross-sectional area at the restriction.
ρ is the density of gas volume at port A, port B, or restriction R, as indicated by the subscript.
The theoretical mass flow rate without nonideal effects is:
where Cd is the discharge coefficient.
Momentum Balance
The pressure difference between ports A and B is based on a momentum balance for flow area contraction between the inlet and the restriction, plus a momentum balance for sudden flow area expansion between the restriction and the outlet.
For flow from port A to port B:
where r is the area ratio, r = SR/S.
For flow from port B to port A:
The pressure differences in the two preceding equations are proportional to the square of the flow rate. This is the typical behavior for turbulent flow. However, for laminar flow, the pressure difference becomes linear with respect to flow rate. The laminar approximation for the pressure difference is:
The threshold for transition from turbulent flow to laminar flow is defined as Δptransition = pavg(1 — Blam), where Blam is the pressure ratio at the transition between laminar and turbulent regimes (Laminar flow pressure ratio parameter value) and pavg = (pA + pB)/2.
The pressure at the restriction is based on a momentum balance for flow area contraction between the inlet and the restriction.
For flow from port A to port B:
For flow from port B to port A:
For laminar flow, the pressure at the restriction is approximately
The block uses a cubic polynomial in terms of (pA – pB) to smoothly blend the pressure difference and the restriction pressure between the turbulent regime and the laminar regime:
When Δptransition ≤ pA – pB,
then pA – pB = ΔpAB
and pR = pRAB.
When 0 ≤ pA – pB < Δptransition,
then pA – pB is smoothly blended between ΔpAB and Δplam
and pR is smoothly blended between pRAB and pRlam.
When –Δptransition < pA – pB ≤ 0,
then pA – pB is smoothly blended between ΔpBA and Δplam
and pR is smoothly blended between pRBA and pRlam.
When pA – pB ≤ –Δptransition,
then pA – pB = ΔpBA
and pR = pRBA.
Choked Flow
When the flow through the restriction becomes choked, further changes to the flow are dependent on the upstream conditions and are independent of the downstream conditions.
If A.p is the Across variable at port A and pBchoked is the hypothetical pressure at port B, assuming choked flow from port A to port B, then
where a is speed of sound.
If B.p is the Across variable at port B and pAchoked is the hypothetical pressure at port A, assuming choked flow from port B to port A, then
The actual pressures at ports A and B, pA and pB, respectively, depend on whether choking has occurred.
For flow from port A to port B, pA = A.p and
For flow from port B to port A, pB = B.p and
Assumptions and Limitations
The restriction is adiabatic. It does not exchange heat with the environment.
This block does not model supersonic flow.
Ports
Input
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2016b



