Local Restriction (TL)
Restriction in flow area in thermal liquid network
Libraries:
Simscape /
Foundation Library /
Thermal Liquid /
Elements
Description
The Local Restriction (TL) block models the pressure drop due to a localized reduction in flow area, such as a valve or an orifice, in a thermal liquid network.
Ports A and B represent the restriction inlet and outlet. The input physical signal at port AR specifies the restriction area. Alternatively, you can specify a fixed restriction area as a block parameter.
The block icon changes depending on the value of the Restriction type parameter.
| Restriction Type | Block Icon |
|---|---|
|
|
|
|
The restriction is adiabatic. It does not exchange heat with the environment.
The restriction consists of a contraction followed by a sudden expansion in flow area. The fluid accelerates during the contraction, causing the pressure to drop. In the expansion zone, if the Pressure recovery check box is cleared, the momentum of the accelerated fluid is lost. If the Pressure recovery check box is selected, the sudden expansion recovers some of the momentum and allows the pressure to rise slightly after the restriction.
Local Restriction Schematic
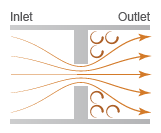
Mass Balance
The mass balance in the restriction is
where:
is the mass flow rate into the restriction through port A.
is the mass flow rate into the restriction through port B.
Momentum Balance
The pressure difference between ports A and B follows from the momentum balance in the restriction:
where:
Δp is the pressure differential.
ρ is the liquid density.
μ is the liquid dynamic viscosity.
S is the cross-sectional area at ports A and B.
SR is the cross-sectional area at the restriction.
vR is fluid velocity at the restriction.
vRc is the critical fluid velocity.
Rec is the critical Reynolds number.
Cd is the discharge coefficient.
If pressure recovery is off, then
where:
pA is the pressure at port A.
pB is the pressure at port B.
If pressure recovery is on, then
Energy Balance
The energy balance in the restriction is
where:
ϕA is the energy flow rate into the restriction through port A.
ϕB is the energy flow rate into the restriction through port B.
Assumptions and Limitations
The restriction is adiabatic. It does not exchange heat with its surroundings.
The dynamic compressibility and thermal capacity of the liquid in the restriction are negligible.
Ports
Input
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2013b



