Phase Detectors: Baud-Rate Type-A Versus Bang-Bang

To successfully send and receive data between a SerDes transmitter and receiver you need to satisfy a myriad of conditions. Chief among these conditions is a synchronization such that the receiver samples the voltage waveform at the correct time instants to recover the message. Typically, the transmitter and receiver have independent oscillators which set the operating frequency of the system within a specified tolerance of each other (for example: 300 parts per million). But the receiver still needs to recover the clock phase and frequency from the waveform signal itself. A clock and data recovery function is accomplished by utilizing a phase detector algorithm and filtering the phase error information to recover the signal phase and frequency.

This example illustrates how first-order phase tracking is accomplished by bang-bang and baud-rate type-A phase detector models.

The bang-bang phase detector is typically found in analog-based SerDes systems where an edge of the eye sampler and a data sampler at the middle of the eye are used together to determine if the data sample is early or late. A sampler is a circuit that can determine if the input voltage is greater than or less than a voltage threshold.

The baud-rate type-A (or Mueller-Muller) phase detector is found in ADC-based SerDes systems where the voltage sample, determined with several bits of precision, and the resolved symbol is used to determine if the sample is early or late.

These two types of phase detectors are not really competitors since they are used in very different types of SerDes systems. This example is as an introduction to these types of phase detectors and their respective advantages and disadvantages.

This example first illustrates how the phase detector models operate in conjunction with decision feedback equalization (DFE) on a pulse response for Statistical analysis and then on sample-by-sample time domain simulations in MATLAB® and Simulink®.

Pulse Response Clock Recovery

When the response of a SerDes system can be reasonably approximated by an impulse response, there is much utility in estimating the system performance through creating the Statistical eye. But first, you need to determine the clock recovery position of the pulse response so that the DFE taps can be properly applied and the Statistical eye can be properly centered.

Baud-Rate Type-A Phase Detector

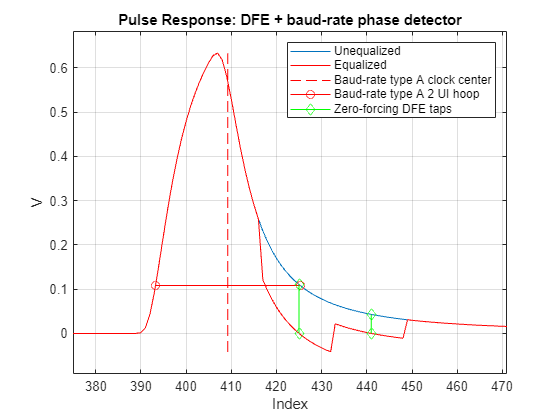
To illustrate how the pulse response clock recovery “hula-hoop” algorithm works, create an example system with a receiver with a DFE which utilizes a baud-rate type-A phase detector. The un-equalized and equalized pulse responses are obtained for visualization purposes. The baud-rate type-A phase detector looks to center the eye such that the pre-cursor and post-cursor ISI are equal. This can be thought of as placing a two-unit interval (UI) wide or two symbol times wide hula-hoop over the unequalized pulse response and sliding it down until it is flat. The clock center is found as the middle of the hula hoop.

% System parameters
SymbolTime = 100e-12;
ModulationLevels = 2;
SamplesPerSymbol = 16;

%Channel parameter
Loss = 8;

%Number of DFE Taps
nTaps = 2;

%Define Receiver and system with BaudRate Type A DFE
rxBaudRate{1} = serdes.DFECDR(...
    'PhaseDetector','BaudRateTypeA',...
    'TapWeights',zeros(1,nTaps));
systemBaudRate = SerdesSystem(...	
	'RxModel',Receiver('Blocks',rxBaudRate),...
    'SamplesPerSymbol',SamplesPerSymbol,...
    'ChannelData',ChannelData('ChannelLossdB',Loss),...
	'SymbolTime',SymbolTime, ...
	'Modulation',ModulationLevels);

%Get unequalized pulse response
pulse_uneq = systemBaudRate.Wave.pulse.uneq;

%Get equalized pulse responses
pulse_BaudRate = systemBaudRate.Wave.pulse.eq;

%Get clock location
phase_BaudRate = systemBaudRate.Wave.outparams{1}.DFECDR.Phase;

%Get DFE tap values
tapsBaudRate = systemBaudRate.Wave.outparams{1}.DFECDR.TapWeights;

%Calculate hula hoop indicies and voltages
ndx_k = 1:length(pulse_uneq);

ndx_BaudRateTypeA = phase_BaudRate*SamplesPerSymbol;
ndx_BaudRateHoop = ndx_BaudRateTypeA + [-1 1]*SamplesPerSymbol;
v_BaudRateHoop = interp1(ndx_k,pulse_uneq,ndx_BaudRateHoop);

%DFE Tap index
ndx_TapsBaudRate = round(ndx_BaudRateTypeA)+SamplesPerSymbol*(1:nTaps);

%Create lines to visualize DFE taps
v_TapsBaudRate = [pulse_uneq(ndx_TapsBaudRate)'; pulse_uneq(ndx_TapsBaudRate)'+tapsBaudRate; nan(1,nTaps) ];

%Find pulse max value, max index and min value (Used to frame the pulse response plot)
[maxValue,maxIndex] = max(pulse_uneq);
minValue = min(pulse_BaudRate);

%Visualize DFE and Baud-rate clock recovery pulse
figure,
plot(ndx_k,pulse_uneq,...
    ndx_k,pulse_BaudRate,'r',...
    ndx_BaudRateTypeA*[1 1],[minValue,maxValue],'r--',...
    ndx_BaudRateHoop,v_BaudRateHoop,'-or',...
    [1;1;1]*ndx_TapsBaudRate,v_TapsBaudRate,'gd-')
axis([maxIndex-2*SamplesPerSymbol,maxIndex+(2+nTaps)*SamplesPerSymbol,minValue-0.05 maxValue + 0.05])
xlabel('Index'),ylabel('V')
title('Pulse Response: DFE + baud-rate phase detector')
grid on
legend('Unequalized','Equalized','Baud-rate type A clock center','Baud-rate type A 2 UI hoop','Zero-forcing DFE taps')

Plot the bathtubs, Statistical Eye and contours for the DFE with a baud-rate phase detector.

figure, plotStatEye(systemBaudRate)
title('Statistical Eye: DFE + baud-rate phase detector')

Bang-Bang Phase Detector

The pulse clock recovery is very similar for the bang-bang phase detector but the hula-hoop width is only one unit interval (UI) wide.

%Define Receiver and system with BangBang DFE
rxBangBang{1} = serdes.DFECDR(...
    'PhaseDetector','BangBang',...
    'TapWeights',zeros(1,nTaps));
systemBangBang = SerdesSystem(...	
	'RxModel',Receiver('Blocks',rxBangBang),...
    'SamplesPerSymbol',SamplesPerSymbol,...
    'ChannelData',ChannelData('ChannelLossdB',Loss),...
	'SymbolTime',SymbolTime, ...
	'Modulation',ModulationLevels);

%Get equalized pulse responses
pulse_BangBang = systemBangBang.Wave.pulse.eq;

%Get clock location
phase_BangBang = systemBangBang.Wave.outparams{1}.DFECDR.Phase;

%Get DFE tap values
tapsBangBang = systemBangBang.Wave.outparams{1}.DFECDR.TapWeights;

%Calculate hula hoop indices and voltages
ndx_BangBang = phase_BangBang*SamplesPerSymbol;
ndx_BangBangHoop = ndx_BangBang + [-0.5 0.5]*SamplesPerSymbol;
v_BangBangHoop = interp1(ndx_k,pulse_uneq,ndx_BangBangHoop);

%DFE Tap index
ndx_TapsBangBang = round(ndx_BangBang)+SamplesPerSymbol*(1:nTaps);

%Create lines to visualize DFE taps
v_TapsBangBang = [pulse_uneq(ndx_TapsBangBang)'; pulse_uneq(ndx_TapsBangBang)'+tapsBangBang; nan(1,nTaps) ];

% 1b) vs Bang Bang in Init
%Plot bathtubs, Statistical Eye and contours
figure,
plot(ndx_k,pulse_uneq,...
    ndx_k,pulse_BangBang,'r',...
    ndx_BangBang*[1 1],[minValue,maxValue],'c--',...
    ndx_BangBangHoop,v_BangBangHoop,'-sc',...
    [1;1;1]*ndx_TapsBangBang,v_TapsBangBang,'gd-')
axis([maxIndex-2*SamplesPerSymbol,maxIndex+(2+nTaps)*SamplesPerSymbol,minValue-0.05 maxValue + 0.05])
grid on
title('Pulse response: DFE + bang-bang phase detector')
legend('Unequalized','Equalized','Bang-bang clock center','Bang-bang 1 UI hoop','Zero-forcing DFE taps')
xlabel('Index'),ylabel('V')

Plot the bathtubs, Statistical Eye and contours for the DFE with a bang-bang phase detector.

figure, plotStatEye(systemBangBang)
title('Statistical Eye: DFE + bang-bang phase detector')

Comparison of Pulse Based Clock Recovery Methods

Comparing the pulse response clock locations for the bang-bang and the baud-rate type-A phase detectors, we observe that the baud-rate type-A clock location is to the right of the bang-bang clock location. This is typically due to the way capacitive loads shape the pulse response. The clock location also impacts the location and value of the zero-forcing DFE tap weights, resulting in significantly different looking Statistical eye diagrams.

Phase Detection of Sample-by-Sample Time Domain Simulation

In an actual system or in a time domain simulation, the system pulse response is not typically available. Therefore, the phase detector must determine if the sampling location is early or late only with the samples of the waveform that it has available. For more information on the bang-bang phase detector use of edge and data samples, see Clock and Data Recovery in SerDes System. The baud-rate type-A phase detector uses voltage sample v[k] (with the precision of a few bits), and the resolved data sample d[k]. The phase error is defined as:

$$\mathrm{Phase}\mathrm{Error}=\mathit{v}\left[\mathit{k}\right]*\mathit{d}\left[\mathit{k}-1\right]-\mathit{v}\left[\mathit{k}-1\right]*\mathit{d}\left[\mathit{k}\right]$$

To visualize how minimizing this phase error results in an optimal sampling location, create a PRBS7 waveform from the unequalized pulse response. Since there are 16 samples per symbol, calculate the baud-rate phase error at 16 different phase locations and compare the sum of each phase error.

%Create PRBS waveform
prbsOrder = 7;
dataPattern = prbs(prbsOrder,2^prbsOrder-1)-0.5;
waveform = pulse2wave(pulse_uneq,dataPattern,SamplesPerSymbol);

wavelength = length(waveform);

%Initialize phase error sum
PhaseErrorSum = zeros(1,SamplesPerSymbol);
for ii = 1:SamplesPerSymbol
    %Index of sample, i.e. "k"
    ndx_k = ii:SamplesPerSymbol:wavelength;

    %Index of prior sample, i.e. "k-1"
    ndx_km1 = mod(ndx_k-SamplesPerSymbol-1,wavelength)+1;

    %Calculate baud-rate type A phase error
    PhaseError = waveform(ndx_k).*sign(waveform(ndx_km1)) - waveform(ndx_km1).*sign(waveform(ndx_k));
    
    %Summarize phase error with its sum
    PhaseErrorSum(ii) = sum(PhaseError);
end

%Determine the index with the minimum phase error sum
[~,minPhaseErrorSumNdx]=min(abs(PhaseErrorSum));

%View the phase error sum for each sample index
figure,
plot(1:SamplesPerSymbol,PhaseErrorSum,'-o',...
    minPhaseErrorSumNdx*[1 1],[min(PhaseErrorSum),max(PhaseErrorSum)],'--')
legend('Sum of phase error','Phase with the minimum phase error')
xlabel('Sample position within eye')
grid on

Now visualize the waveform eye diagram and mark the baud-rate type-A phase position with the minimum phase error.

%Visualize eye and highlight baud-rate type A sample lock location
figure,
    ndx = minPhaseErrorSumNdx:SamplesPerSymbol:wavelength;
    plot(1:SamplesPerSymbol,reshape(waveform,SamplesPerSymbol,[]),'b',...
        minPhaseErrorSumNdx,waveform(ndx),'ro')
    xlabel('Sample position within eye')
    ylabel('V')    
    grid on

Simulink Time-Domain Simulation

With some intuition about the baud-rate type-A phase detector, export the SerDes system to Simulink.

exportToSimulink(systemBaudRate);

Warning: Unrecognized function or variable 'CloneDetectionUI.internal.CloneDetectionPerspective.register'.

Open the Configuration block and click the Open SerDes IBIS-AMI Manager button. On the Export tab, change the Rx Bits to Ignore from 1000 to 10000.

Run the model and note the similarities and differences between the Statistical Eye and the Time Domain Eye.

Downsides of Baud-Rate Phase Detector

Counterintuitively, the baud-rate phase detector requires some residual inter-symbol interference (ISI) to operate properly. If the channel is really clean or if a clock pattern is used, the baud-rate phase detector does not work at all. To observe this, open the Stimulus block parameters dialog box and change the Waveform creation method to Symbol Pattern. Use a Symbol pattern of [0 1]. Also include a 65 ps delay to initialize the phase to the edge of the eye.

In addition to the phase detector being misaligned, the clock pattern invalidates the DFE adaptation assumption of random data.

Observe how the clock within post-simulation time domain analysis eye is nowhere near the optimal position. This shows how the baud-rate phase detector needs some amount of residual ISI for proper operation.

Summary

Analog-based SerDes typically utilize bang-bang phase detectors while ADC-based SerDes utilize baud-rate phase detectors. Each phase detector determines a phase error so that an optimal phase location can be used for recovering the sent information.

Explore Further

• Perform a similar experiment in Simulink with the bang-bang phase detector. Explore how the phase detector works when there is no ISI.

• Look under the mask of the DFECDR block to find the serdes.DFECDR system object. Log the Phase and TapWeights signals and observe the signals in the Simulation Data Inspector. Compare what the baud-rate phase signal does when the clock stimulus is used instead of a random data pattern stimulus.

References

• D. Telian, M. Steinberger, B. Katz, "New SI Techniques for Large System Performance Tuning", Design Con 2016 Conference, San Jose, CA.

• Tyshchenko, O. (2011). Clock and Data Recovery for High-speed ADC-based Receivers (Doctoral dissertation).

• Kurt H. Mueller and Markus Muller. Timing Recovery in Digital Synchronous Data Receivers. IEEE Transactions on Communications, 24(5):516–31, May 1976.

Related Topics

• Clock and Data Recovery in SerDes System