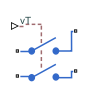
DPST Switch
Double-pole single-throw switch
Libraries:
Simscape /
Electrical /
Switches & Breakers
Description
The DPST Switch block models a double-pole single-throw switch.

When the switch is closed, ports p1 and p2 are connected to ports n1 and n2, respectively.
Closed connections are modeled by a resistor with value equal to the Closed resistance parameter value. Open connections are modeled by a resistor with value equal to the reciprocal of the Open conductance parameter value.
If the Threshold width parameter is set to zero, the switch is closed if the voltage presented at the vT control port exceeds the value of the Threshold parameter.
If the Threshold width parameter is greater than zero, then switch conductance G varies smoothly between off-state and on-state values:
The block uses the function 3λ2 – 2λ3 because its derivative is zero for λ = 0 and λ = 1.
Defining a small positive Threshold width can help solver convergence in some models, particularly if the control port signal vT varies continuously as a function of other network variables. However, defining a nonzero threshold width precludes the solver making use of switched linear optimizations. Therefore, if the rest of your network is switched linear, set Threshold width to zero.
Optionally, you can add a delay between the point at which the voltage at
vT passes the threshold and the switch opening
or closing. To enable the delay, on the Dynamics tab,
set the Model dynamics parameter to Model
turn-on and turn-off times.
Examples
Ports
Refer to the figure for port locations.

Input
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2012b