RegressionPartitionedGAM
Description
RegressionPartitionedGAM is a set of generalized additive models
trained on cross-validated folds. Estimate the quality of the cross-validated regression by
using one or more kfold functions: kfoldPredict,
kfoldLoss, and kfoldfun.
Every kfold object function uses models trained on training-fold (in-fold) observations to predict the response for validation-fold (out-of-fold) observations. For example, suppose you cross-validate using five folds. The software randomly assigns each observation into five groups of equal size (roughly). The training fold contains four of the groups (roughly 4/5 of the data), and the validation fold contains the other group (roughly 1/5 of the data). In this case, cross-validation proceeds as follows:
The software trains the first model (stored in
CVMdl.Trained{1}) by using the observations in the last four groups, and reserves the observations in the first group for validation.The software trains the second model (stored in
CVMdl.Trained{2}) by using the observations in the first group and the last three groups. The software reserves the observations in the second group for validation.The software proceeds in a similar manner for the third, fourth, and fifth models.
If you validate by using kfoldPredict, the software computes
predictions for the observations in group i by using the
ith model. In short, the software estimates a response for every
observation by using the model trained without that observation.
Creation
You can create a RegressionPartitionedGAM model in two ways:
Create a cross-validated model from a GAM object
RegressionGAMby using thecrossvalobject function.Create a cross-validated model by using the
fitrgamfunction and specifying one of the name-value arguments'CrossVal','CVPartition','Holdout','KFold', or'Leaveout'.
Properties
GAM Properties
Flag indicating whether a model for the standard deviation of the response
variable is fit, specified as false or true.
Specify the 'FitStandardDeviation' name-value argument of
fitrgam as true to fit the model for the
standard deviation.
If IsStandardDeviationFit is true, then
you can evaluate the standard deviation at the predictor data X
by using kfoldPredict. This function also returns
the prediction intervals of the response variable, evaluated at
X.
Data Types: logical
Cross-Validation Properties
This property is read-only.
Cross-validated model name, specified as 'GAM'.
This property is read-only.
Number of cross-validated folds, specified as a positive integer.
Data Types: double
This property is read-only.
Cross-validation parameter values, specified as an object. The parameter values
correspond to the values of the name-value arguments used to cross-validate the
generalized additive model. ModelParameters does not contain
estimated parameters.
You can access the properties of ModelParameters using dot
notation.
This property is read-only.
Number of trained trees per model in Trained, specified as a
structure with these fields.
| Field | Value |
|---|---|
PredictorTrees | Numeric vector — Element i in
PredictorTrees indicates the number of trees
per linear term for model i in
Trained. |
InteractionTrees | Numeric vector — Element i in
InteractionTrees indicates the number of
trees per interaction term for model i in
Trained. |
Data Types: struct
This property is read-only.
Data partition indicating how the software splits the data into cross-validation folds, specified as a cvpartition model.
This property is read-only.
Compact models trained on cross-validation folds, specified as a cell array of
CompactRegressionGAM model objects. Trained has
k cells, where k is the number of
folds.
Data Types: cell
Other Regression Properties
This property is read-only.
Categorical predictor
indices, specified as a vector of positive integers. CategoricalPredictors
contains index values indicating that the corresponding predictors are categorical. The index
values are between 1 and p, where p is the number of
predictors used to train the model. If none of the predictors are categorical, then this
property is empty ([]).
Data Types: double
This property is read-only.
Number of observations in the training data stored in X and Y, specified as a numeric scalar.
Data Types: double
This property is read-only.
Predictor variable names, specified as a cell array of character vectors. The order of the
elements in PredictorNames corresponds to the order in which the
predictor names appear in the training data.
Data Types: cell
This property is read-only.
Response variable name, specified as a character vector.
Data Types: char
Response transformation function, specified as "none" or a function handle.
ResponseTransform describes how the software transforms raw
response values.
For a MATLAB® function or a function that you define, enter its function handle. For
example, you can enter Mdl.ResponseTransform =
@function, where
function accepts a numeric vector of the
original responses and returns a numeric vector of the same size containing the
transformed responses.
Data Types: char | string | function_handle
This property is read-only.
Observation weights used to train the model, specified as an n-by-1 numeric
vector. n is the number of observations
(NumObservations).
The software normalizes the observation weights specified in the 'Weights' name-value argument so that the elements of W sum up to 1.
Data Types: double
This property is read-only.
Predictors used to cross-validate the model, specified as a numeric matrix or table.
Each row of X corresponds to one observation, and each column
corresponds to one variable.
Data Types: single | double | table
This property is read-only.
Response used to cross-validate the model, specified as a numeric vector.
Each row of Y represents the observed response of the
corresponding row of X.
Data Types: single | double
Object Functions
kfoldPredict | Predict responses for observations in cross-validated regression model |
kfoldLoss | Loss for cross-validated partitioned regression model |
kfoldfun | Cross-validate function for regression |
Examples
Train a cross-validated GAM with 10 folds, which is the default cross-validation option, by using fitrgam. Then, use kfoldPredict to predict responses for validation-fold observations using a model trained on training-fold observations.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
load carbigCreate a table that contains the predictor variables (Acceleration, Displacement, Horsepower, and Weight) and the response variable (MPG).
tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG);
Create a cross-validated GAM by using the default cross-validation option. Specify the 'CrossVal' name-value argument as 'on'.
rng('default') % For reproducibility CVMdl = fitrgam(tbl,'MPG','CrossVal','on')
CVMdl =
RegressionPartitionedGAM
CrossValidatedModel: 'GAM'
PredictorNames: {'Acceleration' 'Displacement' 'Horsepower' 'Weight'}
ResponseName: 'MPG'
NumObservations: 398
KFold: 10
Partition: [1×1 cvpartition]
NumTrainedPerFold: [1×1 struct]
ResponseTransform: 'none'
IsStandardDeviationFit: 0
Properties, Methods
The fitrgam function creates a RegressionPartitionedGAM model object CVMdl with 10 folds. During cross-validation, the software completes these steps:
Randomly partition the data into 10 sets.
For each set, reserve the set as validation data, and train the model using the other 9 sets.
Store the 10 compact, trained models a in a 10-by-1 cell vector in the
Trainedproperty of the cross-validated model objectRegressionPartitionedGAM.
You can override the default cross-validation setting by using the 'CVPartition', 'Holdout', 'KFold', or 'Leaveout' name-value argument.
Predict responses for the observations in tbl by using kfoldPredict. The function predicts responses for every observation using the model trained without that observation.
yHat = kfoldPredict(CVMdl);
yHat is a numeric vector. Display the first five predicted responses.
yHat(1:5)
ans = 5×1
19.4848
15.7203
15.5742
15.3185
17.8223
Compute the regression loss (mean squared error).
L = kfoldLoss(CVMdl)
L = 17.7248
kfoldLoss returns the average mean squared error over 10 folds.
Train a regression generalized additive model (GAM) by using fitrgam, and create a cross-validated GAM by using crossval and the holdout option. Then, use kfoldPredict to predict responses for validation-fold observations using a model trained on training-fold observations.
Load the patients data set.
load patientsCreate a table that contains the predictor variables (Age, Diastolic, Smoker, Weight, Gender, SelfAssessedHealthStatus) and the response variable (Systolic).
tbl = table(Age,Diastolic,Smoker,Weight,Gender,SelfAssessedHealthStatus,Systolic);
Train a GAM that contains linear terms for predictors.
Mdl = fitrgam(tbl,'Systolic');Mdl is a RegressionGAM model object.
Cross-validate the model by specifying a 30% holdout sample.
rng('default') % For reproducibility CVMdl = crossval(Mdl,'Holdout',0.3)
CVMdl =
RegressionPartitionedGAM
CrossValidatedModel: 'GAM'
PredictorNames: {'Age' 'Diastolic' 'Smoker' 'Weight' 'Gender' 'SelfAssessedHealthStatus'}
CategoricalPredictors: [3 5 6]
ResponseName: 'Systolic'
NumObservations: 100
KFold: 1
Partition: [1×1 cvpartition]
NumTrainedPerFold: [1×1 struct]
ResponseTransform: 'none'
IsStandardDeviationFit: 0
Properties, Methods
The crossval function creates a RegressionPartitionedGAM model object CVMdl with the holdout option. During cross-validation, the software completes these steps:
Randomly select and reserve 30% of the data as validation data, and train the model using the rest of the data.
Store the compact, trained model in the
Trainedproperty of the cross-validated model objectRegressionPartitionedGAM.
You can choose a different cross-validation setting by using the 'CrossVal', 'CVPartition', 'KFold', or 'Leaveout' name-value argument.
Predict responses for the validation-fold observations by using kfoldPredict. The function predicts responses for the validation-fold observations by using the model trained on the training-fold observations. The function assigns NaN to the training-fold observations.
yFit = kfoldPredict(CVMdl);
Find the validation-fold observation indexes, and create a table containing the observation index, observed response values, and predicted response values. Display the first eight rows of the table.
idx = find(~isnan(yFit)); t = table(idx,tbl.Systolic(idx),yFit(idx), ... 'VariableNames',{'Obseraction Index','Observed Value','Predicted Value'}); head(t)
Obseraction Index Observed Value Predicted Value
_________________ ______________ _______________
1 124 130.22
6 121 124.38
7 130 125.26
12 115 117.05
20 125 121.82
22 123 116.99
23 114 107
24 128 122.52
Compute the regression error (mean squared error) for the validation-fold observations.
L = kfoldLoss(CVMdl)
L = 43.8715
Train a cross-validated generalized additive model (GAM) with 10 folds. Then, use kfoldLoss to compute the cumulative cross-validation regression loss (mean squared errors). Use the errors to determine the optimal number of trees per predictor (linear term for predictor) and the optimal number of trees per interaction term.
Alternatively, you can find optimal values of fitrgam name-value arguments by using the OptimizeHyperparameters name-value argument. For an example, see Optimize GAM Using OptimizeHyperparameters.
Load the patients data set.
load patientsCreate a table that contains the predictor variables (Age, Diastolic, Smoker, Weight, Gender, and SelfAssessedHealthStatus) and the response variable (Systolic).
tbl = table(Age,Diastolic,Smoker,Weight,Gender,SelfAssessedHealthStatus,Systolic);
Create a cross-validated GAM by using the default cross-validation option. Specify the 'CrossVal' name-value argument as 'on'. Also, specify to include 5 interaction terms.
rng('default') % For reproducibility CVMdl = fitrgam(tbl,'Systolic','CrossVal','on','Interactions',5);
If you specify 'Mode' as 'cumulative' for kfoldLoss, then the function returns cumulative errors, which are the average errors across all folds obtained using the same number of trees for each fold. Display the number of trees for each fold.
CVMdl.NumTrainedPerFold
ans = struct with fields:
PredictorTrees: [300 300 300 300 300 300 300 300 300 300]
InteractionTrees: [76 100 100 100 100 42 100 100 59 100]
kfoldLoss can compute cumulative errors using up to 300 predictor trees and 42 interaction trees.
Plot the cumulative, 10-fold cross-validated, mean squared errors. Specify 'IncludeInteractions' as false to exclude interaction terms from the computation.
L_noInteractions = kfoldLoss(CVMdl,'Mode','cumulative','IncludeInteractions',false); figure plot(0:min(CVMdl.NumTrainedPerFold.PredictorTrees),L_noInteractions)
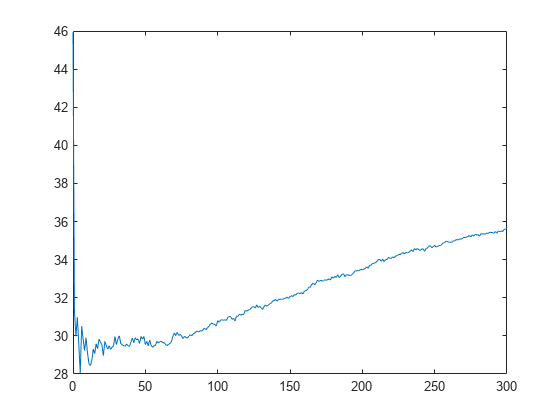
The first element of L_noInteractions is the average error over all folds obtained using only the intercept (constant) term. The (J+1)th element of L_noInteractions is the average error obtained using the intercept term and the first J predictor trees per linear term. Plotting the cumulative loss allows you to monitor how the error changes as the number of predictor trees in the GAM increases.
Find the minimum error and the number of predictor trees used to achieve the minimum error.
[M,I] = min(L_noInteractions)
M = 28.0506
I = 6
The GAM achieves the minimum error when it includes 5 predictor trees.
Compute the cumulative mean squared error using both linear terms and interaction terms.
L = kfoldLoss(CVMdl,'Mode','cumulative'); figure plot(0:min(CVMdl.NumTrainedPerFold.InteractionTrees),L)
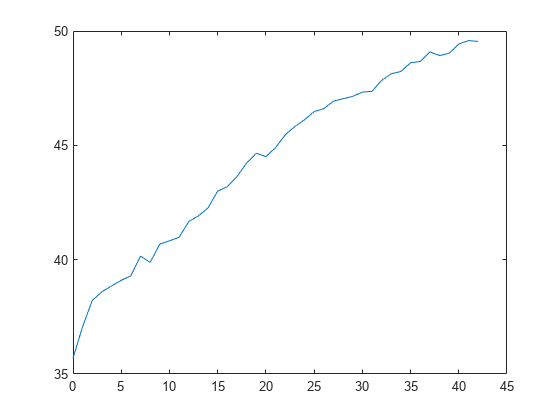
The first element of L is the average error over all folds obtained using the intercept (constant) term and all predictor trees per linear term. The (J+1)th element of L is the average error obtained using the intercept term, all predictor trees per linear term, and the first J interaction trees per interaction term. The plot shows that the error increases when interaction terms are added.
If you are satisfied with the error when the number of predictor trees is 5, you can create a predictive model by training the univariate GAM again and specifying 'NumTreesPerPredictor',5 without cross-validation.
More About
A generalized additive model (GAM) is an interpretable model that explains a response variable using a sum of univariate and bivariate shape functions of predictors.
fitrgam uses a boosted tree as a shape function for each predictor and, optionally, each pair of predictors; therefore, the function can capture a nonlinear relation between a predictor and the response variable. Because contributions of individual shape functions to the prediction (response value) are well separated, the model is easy to interpret.
The standard GAM uses a univariate shape function for each predictor.
where y is a response variable that follows the normal distribution with mean μ and standard deviation σ. g(μ) is an identity link function, and c is an intercept (constant) term. fi(xi) is a univariate shape function for the ith predictor, which is a boosted tree for a linear term for the predictor (predictor tree).
You can include interactions between predictors in a model by adding bivariate shape functions of important interaction terms to the model.
where fij(xixj) is a bivariate shape function for the ith and jth predictors, which is a boosted tree for an interaction term for the predictors (interaction tree).
fitrgam finds important interaction terms based on the p-values of F-tests. For details, see Interaction Term Detection.
If you specify 'FitStandardDeviation' of fitrgam as
false (default), then fitrgam trains a model for
the mean μ. If you specify 'FitStandardDeviation' as
true, then fitrgam trains an additional model
for the standard deviation σ and sets the
IsStandardDeviationFit property of the GAM object to
true.
Version History
Introduced in R2021a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)