Fit Mixed-Effects Spline Regression
This example shows how to fit a mixed-effects linear spline model.
Load the sample data.
load('mespline.mat');This is simulated data.
Plot versus sorted .
[x_sorted,I] = sort(x,'ascend'); plot(x_sorted,y(I),'o')
Fit the following mixed-effects linear spline regression model
where is the th knot, and is the total number of knots. Assume that and .
Define the knots.
k = linspace(0.05,0.95,100);
Define the design matrices.
X = [ones(1000,1),x]; Z = zeros(length(x),length(k)); for j = 1:length(k) Z(:,j) = max(X(:,2) - k(j),0); end
Fit the model with an isotropic covariance structure for the random effects.
lme = fitlmematrix(X,y,Z,[],'CovariancePattern','Isotropic');
Fit a fixed-effects only model.
X = [X Z]; lme_fixed = fitlmematrix(X,y,[],[]);
Compare lme_fixed and lme via a simulated likelihood ratio test.
compare(lme,lme_fixed,'NSim',500,'CheckNesting',true)
ans =
Simulated Likelihood Ratio Test: Nsim = 500, Alpha = 0.05
Model DF AIC BIC LogLik LRStat pValue Lower Upper
lme 4 170.62 190.25 -81.309
lme_fixed 103 113.38 618.88 46.309 255.24 0.68064 0.63784 0.72129
The -value indicates that the fixed-effects only model is not a better fit than the mixed-effects spline regression model.
Plot the fitted values from both models on top of the original response data.
R = response(lme); figure(); plot(x_sorted,R(I),'o', 'MarkerFaceColor',[0.8,0.8,0.8],... 'MarkerEdgeColor',[0.8,0.8,0.8],'MarkerSize',4); hold on F = fitted(lme); F_fixed = fitted(lme_fixed); plot(x_sorted,F(I),'b'); plot(x_sorted,F_fixed(I),'r'); legend('data','mixed effects','fixed effects','Location','NorthWest') xlabel('sorted x values'); ylabel('y'); hold off
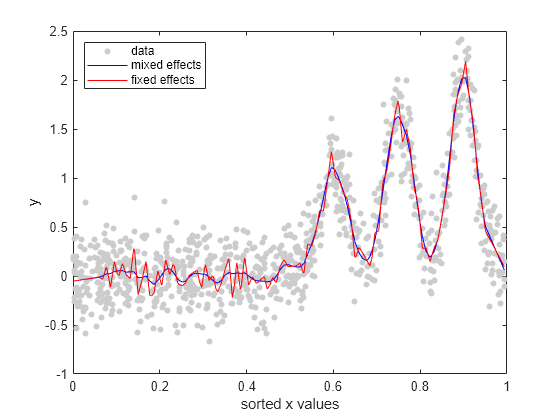
You can also see from the figure that the mixed-effects model provides a better fit to data than the fixed-effects only model.