airy
Airy function
Description
airy( returns the Airy function of
the first kind, Ai(x),
for each element of x)x.
airy(0, is the same
as x)airy(x).
airy(2, returns
the Airy function of
the second kind, Bi(x).x)
airy(___,1) returns the Scaled Airy Functions following the syntax
for the MATLAB® airy function.
Examples
Find the Airy Function of the First Kind
Find the Airy function of the first kind, Ai(x),
for numeric or symbolic inputs using airy. Approximate
exact symbolic outputs using vpa.
Find the Airy function of the first kind, Ai(x),
at 1.5. Because the input is double and not symbolic,
you get a double result.
airy(1.5)
ans =
0.0717Find the Airy function of the values of vector v symbolically,
by converting v to symbolic form using sym.
Because the input is symbolic, airy returns exact
symbolic results. The exact symbolic results for most symbolic inputs
are unresolved function calls.
v = sym([-1 0 25.1 1+1i]); vAiry = airy(v)
vAiry = [ airy(0, -1), 3^(1/3)/(3*gamma(2/3)), airy(0, 251/10), airy(0, 1 + 1i)]
Numerically approximate the exact symbolic result using vpa.
vpa(vAiry)
ans = [ 0.53556088329235211879951656563887, 0.35502805388781723926006318600418,... 4.9152763177499054787371976959487e-38,... 0.060458308371838149196532978116646 - 0.15188956587718140235494791259223i]
Find the Airy function, Ai(x),
of the symbolic input x^2. For symbolic expressions, airy returns
an unresolved call.
syms x airy(x^2)
ans = airy(0, x^2)
Find the Airy Function of the Second Kind
Find the Airy function of the second kind, Bi(x),
of the symbolic input [-3 4 1+1i x^2] by specifying
the first argument as 2. Because the input is symbolic, airy returns
exact symbolic results. The exact symbolic results for most symbolic
inputs are unresolved function calls.
v = sym([-3 4 1+1i x^2]); vAiry = airy(2, v)
vAiry = [ airy(2, -3), airy(2, 4), airy(2, 1 + 1i), airy(2, x^2)]
Use the syntax airy(2,x) like airy(x),
as described in the example Find the Airy Function of the First Kind.
Plot Airy Functions
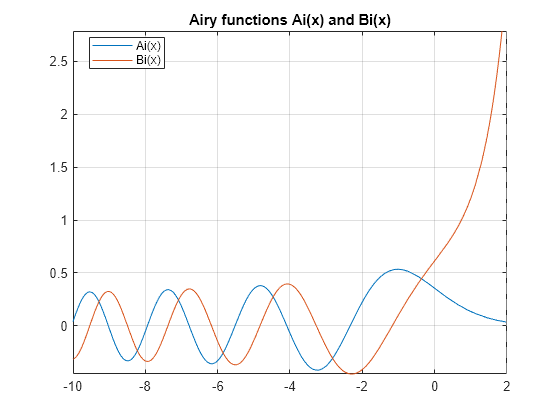
Plot the Airy Functions, and , over the interval [-10 2] using fplot.
syms x fplot(airy(x), [-10 2]) hold on fplot(airy(2,x), [-10 2]) legend('Ai(x)','Bi(x)','Location','Best') title('Airy functions Ai(x) and Bi(x)') grid on hold off
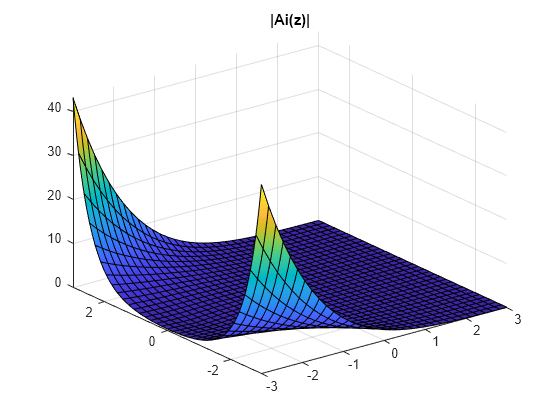
Plot the absolute value of over the complex plane.
syms y z = x + 1i*y; fsurf(abs(airy(z)),[-3 3 -3 3]) title('|Ai(z)|')
Find Derivatives of Airy Functions
Find the derivative of the Airy function of
the first kind, Ai′(x),
at 0 by specifying the first argument of airy as 1.
Then, numerically approximate the derivative using vpa.
dAi = airy(1, sym(0)) dAi_vpa = vpa(dAi)
dAi = -(3^(1/6)*gamma(2/3))/(2*pi) dAi_vpa = -0.2588194037928067984051835601892
Find the derivative of the Airy function of the second kind, Bi′(x),
at x by specifying the first argument as 3.
Then, find the derivative at x =
5 by substituting for x using subs and
calling vpa.
syms x dBi = airy(3, x) dBi_vpa = vpa(subs(dBi, x, 5))
dBi = airy(3, x) dBi_vpa = 1435.8190802179825186717212380046
Solve Airy Differential Equation for Airy Functions
Show that the Airy functions Ai(x) and Bi(x) are the solutions of the differential equation
syms y(x) dsolve(diff(y, 2) - x*y == 0)
ans = C1*airy(0, x) + C2*airy(2, x)
Differentiate Airy Functions
Differentiate expressions containing airy.
syms x y diff(airy(x^2)) diff(diff(airy(3, x^2 + x*y -y^2), x), y)
ans = 2*x*airy(1, x^2) ans = airy(2, x^2 + x*y - y^2)*(x^2 + x*y - y^2) +... airy(2, x^2 + x*y - y^2)*(x - 2*y)*(2*x + y) +... airy(3, x^2 + x*y - y^2)*(x - 2*y)*(2*x + y)*(x^2 + x*y - y^2)
Expand Airy Function using Taylor Series
Find the Taylor series expansion of the Airy
functions, Ai(x) and Bi(x),
using taylor.
aiTaylor = taylor(airy(x)) biTaylor = taylor(airy(2, x))
aiTaylor = - (3^(1/6)*gamma(2/3)*x^4)/(24*pi) + (3^(1/3)*x^3)/(18*gamma(2/3))... - (3^(1/6)*gamma(2/3)*x)/(2*pi) + 3^(1/3)/(3*gamma(2/3)) biTaylor = (3^(2/3)*gamma(2/3)*x^4)/(24*pi) + (3^(5/6)*x^3)/(18*gamma(2/3))... + (3^(2/3)*gamma(2/3)*x)/(2*pi) + 3^(5/6)/(3*gamma(2/3))
Fourier Transform of Airy Function
Find the Fourier transform of the Airy function Ai(x) using fourier.
syms x aiFourier = fourier(airy(x))
aiFourier = exp((w^3*1i)/3)
Numeric Roots of Airy Function
Find a root of the Airy function Ai(x) numerically
using vpasolve.
syms x vpasolve(airy(x) == 0, x)
ans = -226.99630507523600716771890962744
Find a root in the interval [-5 -3].
vpasolve(airy(x) == 0, x, [-5 -3])
ans = -4.0879494441309706166369887014574
Input Arguments
More About
Tips
When you call
airyfor inputs that are not symbolic objects, you call the MATLABairyfunction.When you call
airy(n, x), at least one argument must be a scalar or both arguments must be vectors or matrices of the same size. If one argument is a scalar and the other is a vector or matrix,airy(n,x)expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to the scalar.airyreturns special exact values at0.
Version History
Introduced in R2012a
