Main Content

lsaModel

Latent semantic analysis (LSA) model

expand all in page

Description

A latent semantic analysis (LSA) model discovers relationships between documents and the words that they contain. An LSA model is a dimensionality reduction tool useful for running low-dimensional statistical models on high-dimensional word counts. If the model was fit using a bag-of-n-grams model, then the software treats the n-grams as individual words.

Creation

Create an LSA model using the fitlsa function.

Properties

expand all

Number of components, specified as a nonnegative integer. The number of components is the dimensionality of the result vectors. Changing the value of NumComponents changes the length of the resulting vectors, without influencing the initial values. You can only set NumComponents to be less than or equal to the number of components used to fit the LSA model.

Example: 100

Exponent scaling feature component strengths for the DocumentScores and WordScores properties, and the transform function, specified as a nonnegative scalar. The LSA model scales the properties by their singular values (feature strengths), with an exponent of FeatureStrengthExponent/2.

Example: 2.5

Component weights, specified as a numeric vector. The component weights of an LSA model are the singular values, squared. ComponentWeights is a 1-by-NumComponents vector where the jth entry corresponds to the weight of component j. The components are ordered by decreasing weights. You can use the weights to estimate the importance of components.

Score vectors per input document, specified as a matrix. The document scores of an LSA model are the score vectors in lower dimensional space of each document used to fit the LSA model. DocumentScores is a D-by-NumComponents matrix where D is the number of documents used to fit the LSA model. The (i,j)th entry of DocumentScores corresponds to the score of component j in document i.

Word scores per component, specified as a matrix. The word scores of an LSA model are the scores of each word in each component of the LSA model. WordScores is a V-by-NumComponents matrix where V is the number of words in Vocabulary. The (v,j)th entry of WordScores corresponds to the score of word v in component j.

Unique words in the model, specified as a string vector.

Data Types: string

Object Functions

transformTransform documents into lower-dimensional space

Examples

collapse all

Open Live Script

Fit a Latent Semantic Analysis model to a collection of documents.

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Create a bag-of-words model using bagOfWords.

bag = bagOfWords(documents) 
bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    ...    ] (1x3092 string)
        NumWords: 3092
    NumDocuments: 154

Fit an LSA model with 20 components.

numComponents = 20;
mdl = fitlsa(bag,numComponents)
mdl = 
  lsaModel with properties:

              NumComponents: 20
           ComponentWeights: [2.7866e+03 515.5889 443.6428 316.4191 295.4065 261.8927 226.1649 186.2160 170.6413 156.6033 151.5275 146.2553 141.6741 135.5318 134.1694 128.9931 124.2382 122.2931 116.5035 116.2590]
             DocumentScores: [154x20 double]
                 WordScores: [3092x20 double]
                 Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    ...    ] (1x3092 string)
    FeatureStrengthExponent: 2

Transform new documents into lower dimensional space using the LSA model.

newDocuments = tokenizedDocument([
    "what's in a name? a rose by any other name would smell as sweet."
    "if music be the food of love, play on."]);
dscores = transform(mdl,newDocuments)
dscores = 2×20

    0.1338    0.1623    0.1680   -0.0541   -0.2464    0.0134   -0.2604   -0.0205    0.1127    0.0627    0.3311   -0.2327    0.1689   -0.2695    0.0228    0.1241    0.1198    0.2535   -0.0607    0.0305
    0.2547    0.5576   -0.0095    0.5660   -0.0643    0.1236    0.0082    0.0522   -0.0690   -0.0330    0.0385    0.0803   -0.0373    0.0384   -0.0005    0.1943    0.0207    0.0278    0.0001   -0.0469
Open Live Script

Create a bag-of-words model from some text data.

str = [
    "I enjoy ham, eggs and bacon for breakfast."
    "I sometimes skip breakfast."
    "I eat eggs and ham for dinner."
    ];
documents = tokenizedDocument(str);
bag = bagOfWords(documents);

Fit an LSA model with two components. Set the feature strength exponent to 0.5. 

numComponents = 2;
exponent = 0.5;
mdl = fitlsa(bag,numComponents, ...
    'FeatureStrengthExponent',exponent)
mdl = 
  lsaModel with properties:

              NumComponents: 2
           ComponentWeights: [16.2268 4.0000]
             DocumentScores: [3x2 double]
                 WordScores: [14x2 double]
                 Vocabulary: ["I"    "enjoy"    "ham"    ","    "eggs"    "and"    "bacon"    "for"    "breakfast"    "."    "sometimes"    "skip"    "eat"    "dinner"]
    FeatureStrengthExponent: 0.5000

Calculate the cosine distance between the documents score vectors using pdist. View the distances in a matrix D using squareform. D(i,j) denotes the distance between document i and j.

dscores = mdl.DocumentScores;
distances = pdist(dscores,'cosine');
D = squareform(distances)
D = 3×3

         0    0.6244    0.1489
    0.6244         0    1.1670
    0.1489    1.1670         0

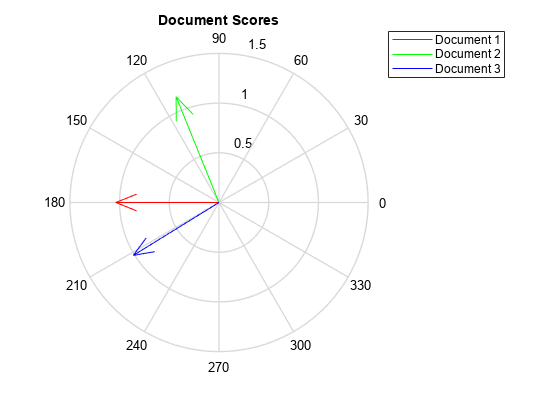
Visualize the similarity between documents by plotting the document score vectors in a compass plot.

figure
compass(dscores(1,1),dscores(1,2),'red')
hold on
compass(dscores(2,1),dscores(2,2),'green')
compass(dscores(3,1),dscores(3,2),'blue')
hold off
title("Document Scores")
legend(["Document 1" "Document 2" "Document 3"],'Location','bestoutside')

Version History

Introduced in R2017b

See Also

| | |

Topics