Optimal finite-difference coefficients for staggered grid finite-differences
Various problems in science and engineering require a finite-difference approximation to first order derivatives on a staggered grid, for example in seismic wave modelling. Such finite-differences use points at ±[0.5,1.5,2.5,...]dx away from the evaluated point. A first order example is given below, with a stencil of just one half point to the left and right:
f'(x) = [f(x+1/2dx) - f(x-1/2dx)]/dx.
The coefficients for longer finite-difference stencils are typically (at an introductory level) derived from Taylor series expansion, which provides a 'spectrally' accurate derivative up to a limited wavenumber. Beyond this critical wavenumber, we cannot properly compute the derivative. To increase the wavenumber-performance of the finite-difference method we then need larger stencils, i.e., a set of even higher-order finite-difference coefficients.
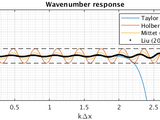
An alternative to using even longer finite-difference stencils, is to use 'optimized' finite-difference coefficients. These coefficients trade off small errors in the lower wavenumber range to gain an enlarged wavenumber range in which the computed derivative is 'approximately' correct. Such coefficients can be designed in various ways, and a large amount of literature exists on the topic. I have implemented two different 'optimized' coefficient algorithms, differing mostly in their behaviour at k=0 (constant functions). Holberg (1987) allows the error at k=0 to be maximum, thereby achieving the largest wavenumber range theoretically possible. Kindelan et al (1990) offer an alternative way to solve this system. Liu (2014) allows no error at k=0, thereby solving for a wavenumber range slightly smaller than that achieved by Holberg (1987). Another paper from Mittet & Arntsen (2000) falls right in between these two approaches by solving Holberg (1987)'s objective function in a least-squares sense.
As an example, we use a 10-point stencil (5 on either side of the point in question) and allow derivative group-errors of 0.3%. With Taylor's coefficients, this requires 4.6 nodes per minimum wavelength; Liu (2014)'s coefficients require 3.04 nodes per minimum wavelength; Mittet & Arntsen (2000)'s coefficients require 2.99 points per wavelength; with Holberg (1987)'s (and Kindelan et al. (1990)'s) coefficients we require 2.91 nodes per minimum wavelength. We can run this example by executing:
>> deriv1_staggered_coeffs(5,0.003)
using the supplied files.
The code provided in this submission designs these Holberg (1987), Mittet & Arntsen (2000) and Liu (2014) coefficients, using the Optimization Toolbox.
These codes are my own implementations based on the aviailable literature:
Holberg (1987): https://doi.org/10.1111/j.1365-2478.1987.tb00841.x
Kindelan, Kamel & Sguazzero (1990): https://library.seg.org/doi/pdf/10.1190/1.1442763
Mittet & Arntsen (2000): http://www.ipt.ntnu.no/~barn/Myarticles/Mittet2000b.pdf
Liu (2014): https://doi.org/10.1093/gji/ggu032
My implementation of Holberg's algorithm is more exact within the given bounds than that suggested in his original paper (Fig. 4, right-most plots, are all supposed to go between ±0.03, but for higher orders seem not to do so...), also because I take the objective function to the power 6 rather than 4. My implementation of Kindelan's algorithm is slightly more overdetermined than that described in the paper, I found no other way to make it work well for any operator-length.
Cite As
Erik Koene (2024). Optimal finite-difference coefficients for staggered grid finite-differences (https://www.mathworks.com/matlabcentral/fileexchange/67259-optimal-finite-difference-coefficients-for-staggered-grid-finite-differences), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.