raytrace
Display or compute RF propagation rays
Description
The raytrace function plots or computes propagation
paths by using ray tracing with surface geometry defined by the Map argument. The function color-codes each propagation path according
to the received power (dBm) or path loss (dB) from the transmitter site to the receiver
site. The ray tracing analysis includes surface reflections and edge diffractions, but
does not include effects from corner diffraction, refraction, or diffuse scattering.
This function supports frequencies from 100 MHz to 100 GHz. For more information, see
Choose a Propagation Model.
raytrace(
displays the propagation paths from the transmitter site tx,rx)tx to
the receiver site rx in the current Site Viewer. By default,
the function uses the shooting and bouncing rays (SBR) method, finds paths with up
to two reflections and zero diffractions, and discards paths that are more than 40
dB weaker than the strongest path.
raytrace(
finds propagation paths using the ray tracing propagation model
tx,rx,propmodel)propmodel. Ray tracing propagation models enable you to
specify properties such as the maximum number of reflections and diffractions, path
loss thresholds, and building and terrain materials. Create a ray tracing
propagation model by using the propagationModel function.
raytrace(___,
specifies options using one or more name-value arguments, in addition to any
combination of inputs from the previous syntaxes.Name=Value)
rays = raytrace(___)rays.
Examples
Show reflected propagation paths in Chicago using a ray tracing propagation model.
Launch Site Viewer with buildings in Chicago. For more information about the OpenStreetMap® file, see [1].
viewer = siteviewer(Buildings="chicago.osm");Create a transmitter site and a receiver site near two different buildings.
tx = txsite(Latitude=41.8800, ... Longitude=-87.6295, ... TransmitterFrequency=2.5e9); show(tx) rx = rxsite(Latitude=41.8813452, ... Longitude=-87.629771, ... AntennaHeight=30); show(rx)
Show the obstruction to the line-of-sight path.
los(tx,rx)

Display propagation paths with reflections. By default, the raytrace function uses the SBR method and calculates propagation paths with up to two reflections.
raytrace(tx,rx)

Appendix
[1] The OpenStreetMap file is downloaded from https://www.openstreetmap.org, which provides access to crowd-sourced map data all over the world. The data is licensed under the Open Data Commons Open Database License (ODbL), https://opendatacommons.org/licenses/odbl/.
Launch Site Viewer with buildings in Chicago. For more information about the OpenStreetMap® file, see [1].
viewer = siteviewer(Buildings="chicago.osm");
Create a transmitter site on a building.
tx = txsite(Latitude=41.8800, ... Longitude=-87.6295, ... TransmitterFrequency=2.5e9);
Create a receiver site near another building.
rx = rxsite(Latitude=41.881352, ... Longitude=-87.629771, ... AntennaHeight=30);
Create a ray tracing propagation model, which MATLAB® represents using a RayTracing object. By default, the propagation model uses the SBR method and finds propagation paths with up to two surface reflections.
pm = propagationModel("raytracing");Calculate the signal strength using the receiver site, the transmitter site, and the propagation model.
ssTwoReflections = sigstrength(rx,tx,pm)
ssTwoReflections = -54.3151
Plot the propagation paths.
raytrace(tx,rx,pm)

Change the RayTracing object to find paths with up to 5 reflections. Then, recalculate the signal strength.
pm.MaxNumReflections = 5; ssFiveReflections = sigstrength(rx,tx,pm)
ssFiveReflections = -53.3965
By default, RayTracing objects use concrete terrain materials and building materials derived from the OpenStreetMap file. When the OpenStreetMap file does not specify materials, the model uses concrete. Change the building and terrain material types to model perfect electrical conductors.
pm.TerrainMaterial = "PEC"; pm.BuildingsMaterial = "PEC"; ssPerfect = sigstrength(rx,tx,pm)
ssPerfect = -38.9334
Plot the propagation paths for the updated propagation model.
raytrace(tx,rx,pm)

Appendix
[1] The OpenStreetMap file is downloaded from https://www.openstreetmap.org, which provides access to crowd-sourced map data all over the world. The data is licensed under the Open Data Commons Open Database License (ODbL), https://opendatacommons.org/licenses/odbl/.
Launch Site Viewer with buildings in Hong Kong. For more information about the OpenStreetMap® file, see [1].
viewer = siteviewer(Buildings="hongkong.osm");
Create transmitter and receiver sites that model a small cell scenario in a dense urban environment.
tx = txsite(Name="Small cell transmitter", ... Latitude=22.2789, ... Longitude=114.1625, ... AntennaHeight=10, ... TransmitterPower=5, ... TransmitterFrequency=28e9); rx = rxsite(Name="Small cell receiver", ... Latitude=22.2799, ... Longitude=114.1617, ... AntennaHeight=1);
Create a ray tracing propagation model, which MATLAB represents using a RayTracing object. Configure the model to use a low average number of degrees between launched rays, to find paths with up to 5 path reflections, and to use building and terrain material types that model perfect electrical conductors. By default, the model uses the SBR method.
pm = propagationModel("raytracing", ... MaxNumReflections=5, ... AngularSeparation="low", ... BuildingsMaterial="PEC", ... TerrainMaterial="PEC");
Visualize the propagation paths and calculate the corresponding path losses.
raytrace(tx,rx,pm,Type="pathloss") raysPerfect = raytrace(tx,rx,pm,Type="pathloss"); plPerfect = [raysPerfect{1}.PathLoss]
plPerfect = 1×13
104.2656 103.5699 112.0092 109.3137 111.2840 111.9979 112.4416 108.1505 111.2825 111.3905 117.7506 116.5906 117.7638

Set the building and terrain material types to glass and concrete, respectively. Then, revisualize the propagation paths and recalculate the corresponding path losses. The model finds one fewer path because, by default, the model discards paths that are more than 40 decibels weaker than the strongest path. The first path loss value does not change because it corresponds to the line-of-sight propagation path.
pm.BuildingsMaterial = "glass"; pm.TerrainMaterial = "concrete"; raytrace(tx,rx,pm,Type="pathloss") raysMtrls = raytrace(tx,rx,pm,Type="pathloss"); plMtrls = [raysMtrls{1}.PathLoss]
plMtrls = 1×12
104.2656 106.1249 119.2135 121.2269 122.3753 121.5228 126.8929 124.1284 122.7842 127.4910 138.9922 140.4998

Incorporate atmospheric loss by adding rain and gas propagation models to the ray tracing model. Then, revisualize the propagation paths and recalculate the corresponding path losses.
pm = pm + propagationModel("rain") + propagationModel("gas"); raytrace(tx,rx,pm,Type="pathloss") raysAtmospheric = raytrace(tx,rx,pm,Type="pathloss"); plAtmospheric = [raysAtmospheric{1}.PathLoss]
plAtmospheric = 1×12
105.3245 107.1846 121.7988 123.1224 124.9622 124.1119 129.6107 126.0247 125.3746 130.2090 142.9753 144.4831

Appendix
[1] The OpenStreetMap file is downloaded from https://www.openstreetmap.org, which provides access to crowd-sourced map data all over the world. The data is licensed under the Open Data Commons Open Database License (ODbL), https://opendatacommons.org/licenses/odbl/.
This example shows how to:
Scale an STL file so that the model uses units of meters.
View the scaled model in Site Viewer.
Use ray tracing to calculate and display propagation paths from a transmitter to a receiver.
While Cartesian txsite and rxsite objects require position coordinates in meters, STL files can use other units. If your STL file does not use meters, you must scale the model before importing it into Site Viewer.
Import and view an STL file. The file models a small conference room with one table and four chairs. Scale the model by specifying the SceneModelScale name-value argument. For this example, assume that the conversion factor from the STL units to meters is 0.9.
viewer = siteviewer(SceneModel="conferenceroom.stl",SceneModelScale=0.9);
Before R2023b: Read the model into a triangulation object by using the stlread function, scale the coordinates and create a new triangulation object, and then read the new triangulation object into Site Viewer.
Create and display a transmitter site close to the wall and a receiver site under the table. Specify the position using Cartesian coordinates in meters.
tx = txsite("cartesian", ... AntennaPosition=[-1.25; -1.25; 1.9], ... TransmitterFrequency=2.8e9); show(tx,ShowAntennaHeight=false) rx = rxsite("cartesian", ... AntennaPosition=[0.3; 0.2; 0.5]); show(rx,ShowAntennaHeight=false)
Pan by left-clicking, zoom by right-clicking or by using the scroll wheel, and rotate the visualization by clicking the middle button and dragging or by pressing Ctrl and left-clicking and dragging.

Create a ray tracing propagation model for Cartesian coordinates, which MATLAB represents using a RayTracing object. Calculate rays that have up to 1 reflection and 1 diffraction. Set the surface material to wood. By default, the model uses the SBR method.
pm = propagationModel("raytracing", ... CoordinateSystem="cartesian", .... MaxNumReflections=1, ... MaxNumDiffractions=1, ... SurfaceMaterial="wood");
Calculate the propagation paths and return the result as a cell array of comm.Ray objects. Extract and plot the rays.
r = raytrace(tx,rx,pm);
r = r{1};
plot(r)View information about a ray by clicking on it.

Since R2023b
View a 3-D model from a glTF™ file created using RoadRunner. RoadRunner is an interactive editor that lets you design 3-D scenes for simulating and testing automated driving systems.
Create a temporary folder to store a sample glTF file. Download the file into the folder by using the downloadGLTFFile helper function. The helper function is attached to the example as a supporting file.
dataDir = fullfile(tempdir,"IntersectionAndBuildings"); if ~exist(dataDir,"dir") mkdir(dataDir) end downloadGLTFFile(dataDir)
Downloading glTF file. Done.
Specify the name of the binary file. Then, import and view the glTF file using Site Viewer. Site Viewer displays the model using the colors and textures stored in the file.
filename = fullfile(dataDir,"IntersectionAndBuildings.glb");
viewer = siteviewer(SceneModel=filename,ShowEdges=false,ShowOrigin=false);
Site Viewer assigns materials to the surfaces in the scene by matching each material name stored in the file with the name of a supported material. View a subset of the materials and matched materials. By default, ray tracing analysis functions use the materials stored in the MatchedCatalogMaterial variable.
viewer.Materials(1:5,:)
ans=5×2 table
Material MatchedCatalogMaterial
______________ ______________________
"Metal_Trim" "metal"
"Glass" "glass"
"Stone_Trim" "marble"
"Roof_Asphalt" "concrete"
"Bricks_Red" "brick"
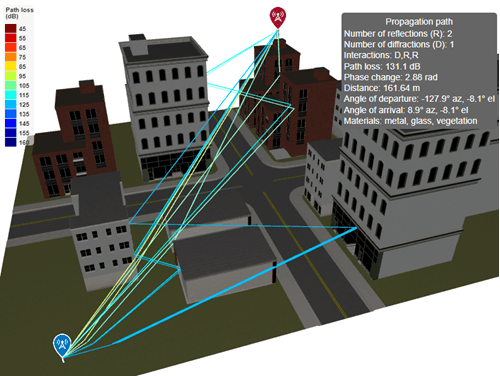
Create a transmitter site above a building and a receiver site behind a cluster of buildings. Specify the positions using Cartesian coordinates in meters.
tx = txsite("cartesian",AntennaPosition=[18;38;22]); rx = rxsite("cartesian",AntennaPosition=[-40;-35;1]);
Create a ray tracing propagation model for Cartesian coordinates, which MATLAB® represents by using a RayTracing object. Configure the model to find propagation paths that have up to two reflections (the default) and one diffraction.
pm = propagationModel("raytracing", ... CoordinateSystem="cartesian", ... MaxNumDiffractions=1);
Calculate the propagation paths and return the result as a cell array of comm.Ray objects. Extract the propagation paths from the cell array.
rays = raytrace(tx,rx,pm);
rays = rays{1};Display the transmitter site, the receiver site, and the propagation paths.
show(tx) show(rx) plot(rays)
View information about a path by clicking it. The information box displays the interaction materials.
Input Arguments
Transmitter site, specified as a txsite
object or an array of txsite objects. If you specify an
array, then the function plots propagation paths from each transmitter to
each receiver site.
Receiver site, specified as an rxsite
object or an array of rxsite objects. If you specify an
array, then the function plots propagation paths from each transmitter to
each receiver site.
Ray tracing propagation model, specified as
"raytracing" or as a RayTracing object. The default is
"raytracing", which uses the SBR method, finds paths
with up to two reflections and zero diffractions, and discards paths that
are more than 40 dB weaker than the strongest path.
Create a RayTracing object by using the propagationModel function. RayTracing
objects enable you to specify properties such as the ray tracing method, the
maximum number of reflections and diffractions, path loss thresholds, and
building and terrain materials.
For information about the differences between ray tracing methods, see Choose a Propagation Model.
Data Types: char | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: raytrace(tx,rx,Type="pathloss") color-codes paths based
on path loss.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: raytrace(tx,rx,"Type","pathloss") color-codes paths
based on path loss.
Type of quantity to plot, specified as one of these options:
"power"— Color-code paths based on the received power in dBm."pathloss"— Color-code paths based on path loss in dB.
The function uses a modified version of the Friis transmission equation to calculate received power (in logarithmic units):
where:
Prx is the received power at the receiver.
Ptx is the transmit power specified by the
TransmitterPowerproperty of the transmitter site.Gtx is the absolute antenna gain of the transmitter site in the direction of the angle-of-departure (AoD).
Grx is the absolute antenna gain of the receiver site in the direction of the angle-of-arrival (AoA).
L is the path loss between the transmitter site and the receiver site.
Ltx is the system loss specified by the
SystemLossproperty of the transmitter site.Lrx is the system loss specified by the
SystemLossproperty of the receiver site.
Data Types: char | string
Propagation model, specified as "raytracing" or as
a RayTracing object. The default is
"raytracing", which uses the SBR method, finds
paths with up to two reflections and zero diffractions, and discards
paths that are more than 40 dB weaker than the strongest path.
Create a RayTracing object by using the propagationModel function. RayTracing
objects enable you to specify properties such as the ray tracing method,
the maximum number of reflections and diffractions, path loss
thresholds, and building and terrain materials.
For information about the differences between ray tracing methods, see Choose a Propagation Model.
Data Types: char | string
Color limits for the colormap, specified as a two-element numeric row
vector of the form [min max].
The units and the default value depend on the value of
Type:
"power"– Units are in dBm, and the default value is[-120 -5]."pathloss"– Units are in dB, and the default value is[45 160].
The color limits indicate the values that map to the first and last colors in the colormap. The function does not plot propagation paths with values that are below the minimum color limit.
Data Types: double
Colormap for coloring the propagation paths, specified as a colormap
name or as an M-by-3 array of RGB triplets that
define M individual colors. For more information
about colormap names, see colormap.
Data Types: char | string | double
Show color legend in Site Viewer, specified as a numeric or logical
1 (true) or
0 (false).
Map for visualization or surface data, specified as a siteviewer
object, a triangulation object, a string scalar, or a character vector.
Valid and default values depend on the coordinate system.
| Coordinate System | Valid map values | Default map value |
|---|---|---|
"geographic" |
|
|
"cartesian" |
|
|
a Alignment of boundaries and region labels are a presentation of the feature provided by the data vendors and do not imply endorsement by MathWorks®. | ||
In most cases, if you specify this argument as a value other than a siteviewer or
"none", then you must also specify an output argument.
Data Types: char | string
Output Arguments
Ray configuration, returned as a
M-by-N cell array of comm.Ray
objects, where M is the number of transmitter sites and
N is the number of receiver sites. Each cell element
is a row vector of comm.Ray objects that represent the
propagation paths (rays) found between the corresponding transmitter site
and receiver site.
Within each row vector, the function sorts the comm.Ray
objects alphabetically by the first interaction type. When the first
interaction type for multiple rays is the same, the function sorts according
to the second interaction type and repeats this behavior for succeeding
repeated interaction types. When multiple comm.Ray objects
have the same number and types of interactions in the same order, the
function sorts the objects by increasing propagation distance. If a
line-of-sight path exists, the function includes it as the first
element.
References
[1] International Telecommunications Union Radiocommunication Sector. Effects of Building Materials and Structures on Radiowave Propagation Above About 100MHz. Recommendation P.2040. ITU-R, approved August 23, 2023. https://www.itu.int/rec/R-REC-P.2040/en.
[2] International Telecommunications Union Radiocommunication Sector. Electrical Characteristics of the Surface of the Earth. Recommendation P.527. ITU-R, approved September 27, 2021. https://www.itu.int/rec/R-REC-P.527/en.
[3] Mohr, Peter J., Eite Tiesinga, David B. Newell, and Barry N. Taylor. “Codata Internationally Recommended 2022 Values of the Fundamental Physical Constants.” NIST, May 8, 2024. https://www.nist.gov/publications/codata-internationally-recommended-2022-values-fundamental-physical-constants.
Extended Capabilities
The raytrace function supports ray
tracing analysis on a GPU with these usage notes and limitations:
The function runs on the GPU when you specify a
RayTracingpropagation model object as input and theUseGPUproperty of the object is"on"or"auto".For information about when the GPU can accelerate ray tracing analysis, see the
UseGPUproperty of theRayTracingobject.In some cases, the GPU and local CPU results can differ due to small differences in algorithms and hardware implementations.
For an example that shows how to perform ray tracing analysis on a GPU, see Accelerate Ray Tracing Analysis Using GPU.
Version History
Introduced in R2019bThe raytrace function performs ray tracing analysis using
additional materials. As a result of this change, depending on the materials in the
scene, the raytrace function can return different
propagation rays or rays with different values in R2025a compared to previous
releases.
The raytrace function uses improved algorithms and
constant values.
The SBR method uses additional edges in the scene as candidates for diffraction. As a result, the SBR method can find more rays in R2025a compared to previous releases.
When you specify transmitters and receivers that have polarized antennas from Antenna Toolbox™ or Phased Array System Toolbox™, the function calculates the phase shifts of rays using an improved algorithm that differently incorporates the far-field patterns of the antennas.
The function uses the constant values that are recommended by the 2022 Committee on Data of the International Science Council (CODATA) adjustment of fundamental constants [3]. In previous releases, the function used constant values from International Telecommunication Union Recommendations (ITU-R) P.2040 and P.527.
As a result of these changes, the raytrace function can
return different propagation rays in R2025a compared to previous releases.
The raytrace function models materials using the methods
and equations in ITU-R P.2040-3 [1] and ITU-R P.527-5
through ITU-R P.527-6 [2].
In previous releases, the function used ITU-R P.2040-1. As a result of these
changes, the raytrace function can return different comm.Ray objects
in R2024a compared to previous releases.
The raytrace function performs ray tracing analysis with multiple materials in the same scene when:
You create the scene from a glTF file, and specify the
propmodelinput argument as"raytracing"or aRayTracingpropagation model object with itsSurfaceMaterialproperty set to"auto"(the default).You create the scene from an OpenStreetMap® file or a geospatial table, and you specify the
propmodelinput argument as"raytracing"or aRayTracingpropagation model object with itsBuildingsMaterialproperty set to"auto"(the default).
The raytrace function performs the ray tracing analysis using the
materials stored in the file or table. If the file or table does not specify materials, or
if the file or table specifies a material that the ray tracing analysis does not support,
then the function uses concrete instead of the absent or unsupported material.
As a result, the raytrace function can return different values in
R2023b compared to previous releases. To avoid using the materials stored in the file or
table, create a RayTracing object (by using the propagationModel
function) and set its SurfaceMaterial property to
"plasterboard" and its BuildingsMaterial
property to "concrete". Then, use the object as input to the
raytrace function.
The raytrace function shows improved performance with complex
scenes when you specify a RayTracing
propagation model object that uses the shooting and bouncing rays (SBR) method as
input.
For example, this code finds ray tracing propagation paths between two antenna
sites in an urban scene by using the raytrace function and a
RayTracing object. Create the RayTracing
object by using the propagationModel function. The code that
finds the propagation paths is about 2x faster in R2023b than in R2023a.
function timingTest % Create Site Viewer and sites sv = siteviewer(Buildings="chicago.osm"); tx = txsite(Latitude=41.88,Longitude=-87.6295,TransmitterFrequency=2.5e9); rx = rxsite(Latitude=41.881,Longitude=-87.62951); % Create RayTracing object pm = propagationModel("raytracing",BuildingsMaterial="concrete", ... MaxNumReflections=2,MaxNumDiffractions=2); % Find propagation paths t1 = tic; raytrace(tx,rx,pm) toc(t1) close(sv) end
The approximate execution times are:
R2023b: 252.47 s
R2023a: 502.76 s
This code was timed on a Windows® 10 Intel®
Xeon® CPU W-2133 @ 3.6 GHz test system, by calling the function
timingTest.
The time that MATLAB® requires to perform ray tracing analysis depends on the scene and on
the properties of the RayTracing object, such as the
AngularSeparation, MaxNumDiffractions,
MaxNumReflections,
MaxAbsolutePathLoss, and
MaxRelativePathLoss properties. In some cases, with
moderate values of the MaxAbsolutePathLoss and
MaxRelativePathLoss properties, the ray tracing analysis
can be more than 2x faster in R2023b than in R2023a.
You can download the OpenStreetMap file used in this example from https://www.openstreetmap.org, which provides access to crowd-sourced map data all over the world. The data is licensed under the Open Data Commons Open Database License (ODbL), https://opendatacommons.org/licenses/odbl/.
Ray tracing propagation models discard propagation paths based on path loss
thresholds. By default, when you specify the propmodel input
argument as "raytracing" or a RayTracing
object, the propagation model discards paths that are more than 40 dB weaker than
the strongest path.
As a result, the raytrace function can return different
values in R2023a compared to previous releases. To avoid discarding paths based on
relative path loss thresholds, create a RayTracing object (by using
the propagationModel function) and set its
MaxRelativePathLoss property to Inf.
Then, use the object as input to the raytrace function.
When you find propagation paths by using the raytrace
function with a ray tracing model that uses the shooting and bouncing rays (SBR)
method, MATLAB calculates the results using double-precision floating-point
computations. In previous releases, the function used single-precision
floating-point computations.
As a result, the raytrace function can return different
comm.Ray objects in R2023a compared to previous
releases.
The NumReflections name-value argument has been removed.
Instead, create a propagation model by using the propagationModel function and specify the
MaxNumReflections name-value argument. Then, use the
raytrace function with the propagation model as an input.
This code shows the recommended workflow.
pm = propagationModel("raytracing",MaxNumReflections=3);
rays = raytrace(tx,rx,pm);When you find propagation paths using the SBR method, MATLAB corrects the results so that the geometric accuracy of each path is exact, using single-precision floating-point computations. In previous releases, the paths have approximate geometric accuracy.
For example, this code finds propagation paths between a transmitter and receiver
by using the default SBR method and returns the paths as comm.Ray
objects. In R2022b, the raytrace function finds seven
propagation paths. In earlier releases, the function approximates eight propagation
paths, one of which is a duplicate path.
viewer = siteviewer(Buildings="hongkong.osm"); tx = txsite(Latitude=22.2789,Longitude=114.1625,AntennaHeight=10, ... TransmitterPower=5,TransmitterFrequency=28e9); rx = rxsite(Latitude=22.2799,Longitude=114.1617,AntennaHeight=1); rSBR = raytrace(tx,rx) raytrace(tx,rx)
| R2022b | R2022a |
|---|---|
rSBR =
1×1 cell array
{1×7 comm.Ray}
|
rSBR =
1×1 cell array
{1×8 comm.Ray}
|
Paths calculated using the SBR method in R2022b more closely align with paths calculated using the image method. The image method finds all possible paths with exact geometric accuracy. For example, this code uses the image method to find propagation paths between the same transmitter and receiver.
viewer = siteviewer(Buildings="hongkong.osm"); tx = txsite(Latitude=22.2789,Longitude=114.1625, ... AntennaHeight=10,TransmitterPower=5, ... TransmitterFrequency=28e9); rx = rxsite(Latitude=22.2799,Longitude=114.1617, ... AntennaHeight=1); pm = propagationModel("raytracing",Method="image",MaxNumReflections=2); rImage = raytrace(tx,rx,pm)
rImage =
1×1 cell array
{1×7 comm.Ray}In this case, the SBR method finds the same number of propagation paths as the image method. In general, the SBR method finds a subset of the paths found by the image method. When both the image and SBR methods find the same path, the points along the path are the same within a tolerance of machine precision for single-precision floating-point values.
This code compares the path losses, within a tolerance of
0.0001, calculated by the SBR and image methods.
abs([rSBR{1}.PathLoss]-[rImage{1}.PathLoss]) < 0.0001ans = 1×7 logical array 1 1 1 1 1 1 1
The path losses are the same within the specified tolerance.
As a result, the raytrace function can return different
results in R2022b compared to previous releases.
The function can return a different number of
comm.Rayobjects because it discards invalid or duplicate paths.The function can return different
comm.Rayobjects because it calculates exact paths rather than approximate paths.
The NumReflections name-value argument issues a warning that it
will be removed in a future release.
Starting in R2021b, the raytrace function uses the shooting
and bouncing rays (SBR) method and calculates up to two reflections by default. In
previous releases, the raytrace function uses the image method
and calculates up to one reflection.
To display or compute RF propagation rays using the image method instead, create a
propagation model by using the propagationModel function. Then, use the
raytrace function with the propagation model as input. This
example shows how to update your
code.
pm = propagationModel('raytracing','Method','image'); raytrace(tx,rx,pm)
For information about the SBR and image methods, see Choose a Propagation Model.
Starting in R2021b, all RF Propagation functions use the SBR method by default and calculate up to two reflections. For more information, see Default modeling method is shooting and bouncing rays method.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

