Viterbi Decoder
Decode convolutionally encoded data using Viterbi algorithm
Libraries:
Communications Toolbox /
Error Detection and Correction /
Convolutional
Communications Toolbox HDL Support /
Error Detection and Correction /
Convolutional
Description
The Viterbi Decoder block decodes convolutionally encoded input symbols to produce binary output symbols by using the Viterbi algorithm. A trellis structure specifies the convolutional encoding scheme. For more information, see Trellis Description of a Convolutional Code.
This block can process several symbols at a time for faster performance and can accept inputs that vary in length during simulation. For more information about variable-size signals, see Variable-Size Signal Basics (Simulink).
This icon shows all the optional block ports enabled.
![]()
Examples
Apply convolutional encoding and BPSK modulation to a binary signal, pass the modulated signal through an AWGN channel. Compute the symbol error rate (SER) of the signal after applying BPSK demodulation and Viterbi decoding.
Explore model
The doc_conv model generates a binary signal by using a Bernoulli Binary Generator block. The Convolutional Encoder block encodes the signal. The BPSK Modulator Baseband block modulates the signal. The AWGN Channel block adds noise to the signal. To demodulate the BPSK modulated signal with zero phase shift, simply extract the value of the real component of the complex symbol demodulation by using the Complex to Real-Imag (Simulink) block. The Viterbi Decoder block decodes the signal. The Error Rate Calculation block computes the SER.

Run simulation
ans =
'Filtering the signal through an AWGN channel with the EsN0 set to -1 dB, the computed SER is 0.005608.'
ans =
'For 53499 transmitted symbols, there were 300 symbols errors.'
This example simulates a punctured coding system that uses rate 1/2 convolutional encoding and Viterbi decoding. The complexity of a Viterbi decoder increases rapidly with the code rate. The puncturing technique enables encoding and decoding of higher rate codes by using standard lower rate coders.
The cm_punct_conv_code model transmits a convolutionally encoded BPSK signal through an AWGN channel, demodulates the received signal, and then performs Viterbi decoding to recover the uncoded signal. To compute the error rate, the model compares the original % signal and the decoded signal.

The model uses the PreloadFcn callback function to set these workspace variables for initialization of block parameters:
puncvec = [1;1;0;1;1;0]; EsN0dB = 2; traceback = 96; % Viterbi traceback depth
For more information, see Model Callbacks (Simulink).
The blocks in this model perform these operations:
Bernoulli Binary Generator — Sets Sample per frames to
3. The block creates a sequence of random bits outputting three samples per frame at each sample time.Convolutional Encoder — Uses the default setting for Trellis structure, selects Puncture code, and sets Puncture vector to the workspace variable
puncvec. The block encodes frames of data by puncturing a rate 1/2, constraint length 7 convolutional code to a rate 3/4 code. The puncture vector specified bypuncvecis the optimal puncture vector for the rate 1/2, constraint length 7 convolutional code. A1in the puncture vector indicates that the bit in the corresponding position of the coded vector is sent to the output vector, while a0indicates that the bit is removed. For the configured encoder, coded bits in positions 1, 2, 4, and 5 are transmitted, while bits in positions 3 and 6 are removed. The rate 3/4 code means that for every 3 bits of input, the punctured code generates 4 bits of output.BPSK Modulator Baseband — Modulates the encoded message using default parameter values.
AWGN Channel — Sets Mode to
Signal to noise ratio (Es/No)and setsEs/No (dB)to the workspace variableEsN0dB. Since the modulator block generates unit power signals, Input signal power, referenced to 1 ohm (watts) keeps its default value of1.Viterbi Decoder — Uses settings for Trellis structure, Punctured code, and Puncture vector that align with the Convolutional Encoder block. The block sets Decision type to
Unquantizedand Traceback depth to thetracebackworkspace variable. To decode the specified convolutional code without puncturing the code, a traceback depth of 40 is sufficient. However, to give the decoder enough data to resolve the ambiguities introduced by the punctures, the block uses a traceback depth of 96 to decode the punctured code. Similar to the convolutional encoder, the puncture vector for the decoder indicates the locations of the punctures. For the decoder, the locations are bits to ignore in the decoding process because the punctured bits are not transmitted and there is no information to indicate their values. Each 1 in the puncture vector indicates a transmitted bit, and each 0 indicates a punctured bit to ignore in the input to the decoder.Complex to Real-Imag (Simulink) — Demodulates the BPSK signal by extracting the real part of the complex samples.
Error Rate Calculation — Uses the Receive delay value to account for total number of samples of system delay and compares the decoded bits to the original source bits. The block outputs a three-element vector containing the calculated BER, the number of errors observed, and the number of bits processed. The Receive delay is set to the
tracebackworkspace variable because the Viterbi traceback depth causes the only delay in the system. Typically, BER simulations run until a minimum number of errors have occurred, or until the simulation processes a maximum number of bits. The Error Rate Calculation block selects the Stop simulation parameter and sets the target number of errors to100and the maximum number of symbols to1e6to control the duration of the simulation.
Evaluate Bit Error Rate
Generate a bit error rate curve by running this code to simulate the model over a range of EbN0 settings.
Compare the simulation results with an approximation of the bit error probability bound for a punctured code as per [ 1 ]. The bit error rate performance of a rate 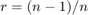 punctured code is bounded above by the expression:
punctured code is bounded above by the expression:

In this expression, erfc denotes the complementary error function,  is the code rate, and both
is the code rate, and both  and
and  are dependent on the particular code. For the rate 3/4 code of this example,
are dependent on the particular code. For the rate 3/4 code of this example,  = 5,
= 5,  = 42,
= 42,  = 201,
= 201,  = 1492, and so on. For more information, see reference [ 1 ].
= 1492, and so on. For more information, see reference [ 1 ].
Compute an approximation of the theoretical bound using the first seven terms of the summation for Eb/N0 values in 2:0.02:5. The values used for nerr come from reference [ 2 ], Table II.
Plot the simulation results, a fitted curve, and theoretical bounds.

In some cases, at the lower bit error rates, you might notice simulation results that appear to indicate error rates slightly above the bound. This result can come from the finite traceback depth in the decoder or, if you observe fewer than 500 bit errors, from simulation variance.
For an example that shows convolutional coding without puncturing, see the Soft-Decision Decoding section in Error Detection and Correction.
References
Yasuda, Y., K. Kashiki, and Y. Hirata, "High Rate Punctured Convolutional Codes for Soft Decision Viterbi Decoding," IEEE Transactions on Communications, Vol. COM-32, March, 1984, pp. 315–319.
Begin, G., Haccoun, D., and Paquin, C., "Further results on High-Rate Punctured Convolutional Codes for Viterbi and Sequential Decoding," IEEE Transactions on Communications, Vol. 38, No. 11, November, 1990, p. 1923.
Use the Viterbi Decoder block for fixed-point hard- and soft-decision convolutional decoding. Compare results to theoretical upper bounds as computed with the Bit Error Rate Analysis app.
Simulation Configuration
The cm_viterbi_harddec_fixpt and cm_viterbi_softdec_fixpt models highlight the fixed-point modeling attributes of the Viterbi decoder, using similar layouts. The default configuration of the models use the PreLoadFcn Callback to specify an  setting of 4 dB for the AWGN Channel block. The convolutional encoder is configured as a rate 1/2 encoder. Specifically, for every 2 bits the encoder adds another 2 redundant bits. To accommodate the code rate, the Eb/No (dB) parameter of the AWGN block is halved by subtracting
setting of 4 dB for the AWGN Channel block. The convolutional encoder is configured as a rate 1/2 encoder. Specifically, for every 2 bits the encoder adds another 2 redundant bits. To accommodate the code rate, the Eb/No (dB) parameter of the AWGN block is halved by subtracting 10*log10(2) from the assigned  setting. To limit the run duration to 100 errors or 1e6 bits for the Error Rate Calculation block.
setting. To limit the run duration to 100 errors or 1e6 bits for the Error Rate Calculation block.
Fixed-Point Modeling
Fixed-point modeling enables bit-true simulations which take into account hardware implementation considerations and the dynamic range of the data and parameters. For example, if the target hardware is a DSP microprocessor, some of the possible word lengths are 8, 16, or 32 bits, whereas if the target hardware is an ASIC or FPGA, there may be more flexibility in the word length selection.
To enable fixed-point Viterbi decoding,
For hard decisions, the block input must be of type ufix1 (unsigned integer of word length 1). Based on this input (either a 0 or a 1), the internal branch metrics are calculated using an unsigned integer of word length = (number of output bits), as specified by the trellis structure (which equals 2 for the hard-decision example).
For soft decisions, the block input must be of type ufixN (unsigned integer of word length N), where N is the number of soft-decision bits, to enable fixed-point decoding. The block inputs must be integers in the range 0 to
 . The internal branch metrics are calculated using an unsigned integer of word length = (N + number of output bits - 1), as specified by the trellis structure (which equals 4 for the soft-decision example).
. The internal branch metrics are calculated using an unsigned integer of word length = (N + number of output bits - 1), as specified by the trellis structure (which equals 4 for the soft-decision example).
The State metric word length is specified by the user and usually must be greater than the branch metric word length already calculated. You can tune this to be the most suitable value (based on hardware and data considerations) by reviewing the logged data for the system.
Enable the logging by selecting Apps > Fixed-Point Tool. In the Fixed-Point Setting menu, set the Fixed-point instruments mode to Minimums, maximums and overflows, and rerun the simulation. If you see overflows, it implies the data did not fit in the selected container. You could either try scaling the data prior to processing it or, if your hardware allows, increase the size of the word length. Based on the minimum and maximum values of the data, you are also able to determine whether the selected container is of the appropriate size.
Try running simulations with different values of State metric word length to get an idea of its effect on the algorithm. You should be able to narrow down the parameter to a suitable value that has no adverse effect on the BER results.
The hard decision configuration for the cm_viterbi_harddec_fixpt model:

The BPSK Demodulator Baseband produces hard decisions, which are passed onto the decoder.
The Data Type Conversion (Simulink) block sets the
Modeparameter toFixed pointand casts the output data type tofixdt(0,1,0). The signal input to the Viterbi Decoder block isufix1.
The Viterbi Decoder block has the
Decision typeparameter set toHard decision, and on the Data Types tab, theState metric word lengthis set to4and theOutput data typeis set toboolean. The bit error rate is displayed and captured to theBERworkspace variable.
The soft decision configuration for the cm_viterbi_softdec_fixpt model:

The BPSK Demodulator Baseband produces soft decisions using the log-likelihood ratio. These soft outputs are 3-bit quantized and passed onto the decoder.
A Quantizer subsystem (containing Gain (Simulink), Scalar Quantizer Encoder, and Data Type Conversion (Simulink) blocks) quantizes the signal and casts the output data type to
fixdt(0,3,0). The signal input to the Viterbi Decoder block isufix3.
The Viterbi Decoder block has the
Decision typeparameter set toSoft decisionandNumber of soft decision bitsset to 3, and on the Data Types tab, theState metric word lengthis set to6and theOutput data typeis set toboolean. The bit error rate is displayed and captured to theBERworkspace variable.
Comparisons Between Hard and Soft-Decision Decoding
The two models are configured to run from within the Bit Error Rate Analysis app to generate simulation curves to compare the BER performance for hard-decision versus soft-decision decoding.
You can produce the results in this plot by following the steps outlined below.

These steps generate simulation results for theoretical and fixed-point hard and soft decision Viterbi decoding:
Open the Bit Error Rate Analysis app by selecting it in the Apps tab or by entering
bertoolat the MATLAB command prompt.On the Theoretical pane, with Eb/N0 range set to 2:5, Channel type set to
AWGN, Modulation type set toPSK, Channel coding set toConvolutional, run with Decision method set toHardand thenSoft. Rename the BER Data Set to identify the hard and soft data sets of theoretical results.On the Monte Carlo pane, set Eb/N0 range to 2:1:5, for Simulation environment select
Simulink, BER variable name set toBER, for Simulation limits set Number of errors to 100 and Number of bits to 1e6. Run with Model name set tocm_viterbi_harddec_fixptand thencm_viterbi_softdec_fixpt. Rename the BER Data Set to identify the hard and soft data sets of Simulink results.
After the four runs the app will resemble this image.

Comparisons with Double-Precision Data
For further explorations, you can run the same model with double precision data by selecting Apps > Fixed-Point Tool. In the Fixed-Point Tool app, select the Data type override to be Double. This selection overrides all data type settings in all the blocks to use double precision. For the Viterbi Decoder block, as Output type was set to boolean, this parameter should also be set to double.
Upon simulating the model, note that the double-precision and fixed-point BER results are the same. They are the same because the fixed-point parameters for the model have been selected to avoid any loss of precision and optimize memory efficiency.
Extended Examples
Tail-Biting Convolutional Coding
Use the Convolutional Encoder and Viterbi Decoder blocks to simulate a tail-biting convolutional code.
Ports
Input
Convolutionally encoded codeword, specified as a column vector. If the
decoder takes N input bit streams (that
is, it can receive 2N possible input symbols), the block input
vector length is L×N for some positive integer L. For more information, see Input and Output Sizes, Input Values and Decision Types, and the Operation mode parameter.
This port is unnamed until a second input port is enabled.
Data Types: double | single | Boolean | int8 | int16 | int32 | uint8 | uint16 | uint32 | ufixn
Erasure bits in the codeword, specified as a binary-valued vector.
Values of 1 in the vector correspond to erased bits,
and values of 0 correspond to nonerased bits.
For these erasures in the incoming data stream, the decoder does not update the branch metric. The widths and the sample times of the erasure and the input data ports must be the same.
Dependencies
To enable this port, select Enable erasures input port.
Data Types: double | Boolean
Option to reset the state of decoder registers, specified as scalar value. When this port receives a nonzero input value, the block sets its internal memory to the initial state before processing the input data. Resetting the decoder registers to the initial state sets:
The all-zeros state metric to zero
All other state metrics to the maximum value
The traceback memory to zero
Using the reset port on this block is analogous to setting
Operation mode for the Convolutional Encoder block
to Reset on nonzero input via port.
Dependencies
To enable this port, set the Operation
mode parameter to
Continuous and select
Enable reset input port.
Data Types: double | Boolean
Output
Output message, returned as a binary column vector. If the decoder produces K output bit streams (that is, it can produce 2K possible output symbols), the block output vector length is L×K for some positive integer L. For more information, see Input and Output Sizes.
This port is unnamed on the block icon.
Data Types: double | single | Boolean | int8 | int16 | int32 | uint8 | uint16 | uint32 | ufix1
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Main
Trellis description of the convolutional code, specified as a structure that contains the trellis description for a rate K ∕ N code. K is the number of input bit streams, and N is the number of output bit streams.
You can either use the poly2trellis function to
create the trellis structure or create it manually. For more about this
structure, see Trellis Description of a Convolutional Code and the
istrellis function.
The trellis structure contains these fields.
Number of symbols input to the encoder, specified as an integer equal to 2K, where K is the number of input bit streams.
Number of symbols output from the encoder, specified as an integer equal to 2N, where N is the number of output bit streams.
Number of states in the encoder, specified as a power of 2.
Next states for all combinations of current states and current inputs, specified
as a matrix of integers. The matrix size must be numStates by
2K.
Outputs for all combinations of current states and current inputs, specified as a matrix of
octal numbers. The matrix size must be numStates by
2K.
Select this parameter to view and enable the Puncture vector parameter.
Puncture pattern vector to puncture the decoded data, specified as a vector. The vector
must contain 1s and 0s, where
0 indicates the position of the punctured bits. This
puncture pattern must match the puncture pattern used by the convolutional
encoder.
For some commonly used puncture patterns for specific rates and polynomials, see the Yasuda [4], Haccoun [5], and Begin [6] references.
Dependencies
This parameter appears only when you select the Punctured code parameter.
Select this parameter to add the Era input port to
the block.
Decoder decision type, specified as
Unquantized, Hard
decision, or Soft Decision.
Unquantized— The decoder uses the Euclidean distance to calculate the branch metrics. The input data must be a real-valued vector of double- or single-precision soft values that are unquantized. The object maps positive values to logical1s and negative values to logical0sHard decision— The decoder uses Hamming distance to calculate the branch metrics. The input must be a vector of hard decision values, which are0s or1s. The data type of the inputs must be double precision, single precision, logical, or numeric.Soft Decision— The decoder uses Hamming distance to calculate the branch metrics. The input requires a vector of quantized soft values that are represented as integers between 0 and 2SoftInputWordLength – 1. The data type of the inputs must be double precision, single precision, logical, or numeric. Alternatively, you can specify the data type as an unsigned and unscaled fixed-point object using thefi(Fixed-Point Designer) object with a word length (SoftInputWordLength) equal to the word length that you specify for the Number of soft decision bits parameter.0is considered as most confident0and 2SoftInputWordLength – 1 as the most confident1.
Soft input word length that represents the number of bits for each quantized soft input value, specified as an integer.
Dependencies
This parameter appears only when you set the Decision type parameter to Soft
decision.
Select this parameter to error if the quantized input values are out of range. If you do not select this parameter, out of range input values are ignored.
Dependencies
This parameter appears only when you set the Decision type parameter to Hard
decision or Soft
decision.
Traceback depth, specified as an integer that indicates the number of trellis branches used to construct each traceback path.
The traceback depth influences the decoding delay. The decoding delay is the number of zero symbols that precede the first decoded symbol in the output.
For the continuous operating mode, the decoding delay is equal to the number of traceback depth symbols.
For the truncated or terminated operating mode, the decoding delay is zero. In this case, the traceback depth must be less than or equal to the number of symbols in each input.
As a general estimate, a typical traceback depth value is approximately two
to three times (ConstraintLength – 1) / (1 –
coderate). The constraint length of the code, ConstraintLength,
is equal to (log2(trellis.numStates) +
1). The coderate is equal to (K / N) ×
(length(PuncturePattern) /
sum(PuncturePattern).
K is the number of input symbols, N is the number of output symbols, and PuncturePattern is the puncture pattern vector.
For example, applying this general estimate, results in these approximate traceback depths.
A rate 1/2 code has a traceback depth of 5(ConstraintLength – 1).
A rate 2/3 code has a traceback depth of 7.5(ConstraintLength – 1).
A rate 3/4 code has a traceback depth of 10(ConstraintLength – 1).
A rate 5/6 code has a traceback depth of 15(ConstraintLength – 1).
For more information, see [7].
Method for transitioning between successive input frames, specified as one of these mode values.
Continuous— The block saves its internal state metric at the end of each input, for use with the next frame. Each traceback path is treated independently. This mode results in a decoding delay of Traceback depth×K zero bits for a rate K/N convolutional code. K is the number of message symbols, and N is the number of coded symbols. If the Enable reset input port is selected, the decoder states are reset if theRstport receives a nonzero value.Truncated— The block treats each input independently. The traceback path starts at the state with the best metric and always ends in all-zeros state. This mode is appropriate when the corresponding Convolutional Encoder block has its Operation mode set toTruncated (reset every frame). There is no output delay for this mode.Terminated— The block treats each input independently, and the traceback path always starts and ends in all-zeros state. This mode is appropriate when the uncoded message signal (that is, the input to the corresponding Convolutional Encoder block) has enough zeros at the end of each input to fill all memory registers of the feed-forward encoder. Specifically, there are at leastk*max(constr-1)zeros at the end of the input, for an encoder that haskinput streams and constraint length vectorconstr(using the polynomial description). For feedback encoders, this mode is appropriate if the corresponding Convolutional Encoder block has Operation mode set toTerminate trellis by appending bits.
Note
The decoder states reset at every input time step when the block
outputs sequences that vary in length during simulation and you set the
Operation mode to
Truncated or
Terminated.
When the input signal contains only one symbol, use the
Continuous operation mode.
Select this parameter to add the Rst input
port.
Dependencies
This parameter appears only when you set the Operation mode parameter to
Continuous.
Select this parameter to delay reset of the decoder until after computing the encoded data received in the current time step. You must enable this option for HDL support. Generating HDL code requires HDL Coder™ software.
Dependencies
This parameter appears only when you set the Operation mode parameter to
Continuous and select Enable
reset input port.
Data Types
State metric word length, specified as a positive integer.
Output data type, specified as double,
single, boolean,
int8, uint8,
int16, uint16,
int32, or uint32, or set to
'Inherit via internal rule' or 'Smallest
unsigned integer'.
When set to
'Smallest unsigned integer', the output data type is selected based on the settings used in the Hardware Implementation pane of the Configuration Parameters dialog box of the model. IfASIC/FPGAis selected in the Hardware Implementation pane, the output data type isufix(1). For all other selections, it is an unsigned integer with the smallest specified word length corresponding to the char value (for example,uint8).When set to
'Inherit via internal rule', the block:Outputs data type double for double inputs
Outputs data type single for single inputs
Behaves similar to the
'Smallest unsigned integer'option for all other data type inputs
Block Characteristics
More About
If the convolutional code uses an alphabet of 2N possible symbols, the input vector length must be L×N for some positive integer L. Similarly, if the decoded data uses an alphabet of 2K possible output symbols, the output vector length is L×K.
This block accepts a column vector input signal with any positive integer value for L. For variable-size inputs, L can vary during simulation. The operation of the block is governed by the operation mode parameter.
This table shows the data types supported for the input and output ports.
| Port | Supported Data Types |
|---|---|
Input |
|
Output |
|
The entries of the input vector are either bipolar real, binary, or integer data, depending on the Decision type parameter.
| Decision type Parameter | Possible Entries in Decoder Input | Interpretation of Values | Branch metric calculation |
|---|---|---|---|
| Real numbers Input values outside of the range [–1012, 1012] are clipped to –1012 and 1012, respectively. | Positive real: logical zero Negative real: logical one | Euclidean distance |
| 0, 1 | 0: logical zero 1: logical one | Hamming distance |
| Integers between 0 and 2 b -1, where b is the Number of soft decision bits parameter. | 0: most confident decision for logical zero 2b-1: most confident decision for logical one Other values represent less confident decisions. | Hamming distance |
To illustrate the soft decision situation more explicitly, the following table lists interpretations of values for 3-bit soft decisions.
| Input Value | Interpretation |
|---|---|
| 0 | Most confident zero |
| 1 | Second most confident zero |
| 2 | Third most confident zero |
| 3 | Least confident zero |
| 4 | Least confident one |
| 5 | Third most confident one |
| 6 | Second most confident one |
| 7 | Most confident one |
There are three main components to the Viterbi decoding algorithm. They are branch metric computation (BMC), add-compare and select (ACS), and traceback decoding (TBD). This diagram illustrates the signal flow for a k/n rate code.

This diagram illustrates the BMC for a 1/2 rate, nsdec = 3 signal flow.
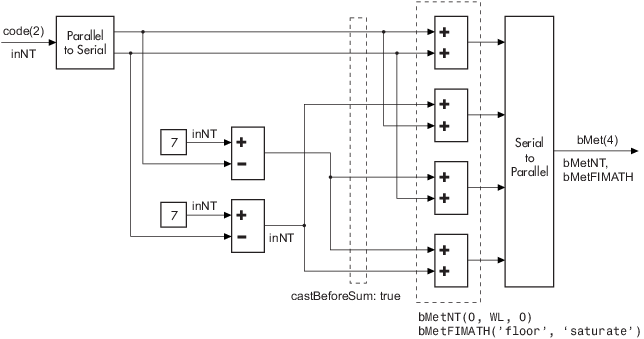
This diagram illustrates an ACS component cycle, where
WL2 is specified on the mask by the user.

In these flow diagrams, inNT, bMetNT , stMetNT, and outNT are numerictype (Fixed-Point Designer) objects, and bMetFIMATH and
stMetFIMATH, are fimath (Fixed-Point Designer)
objects.
References
[1] Clark, George C., and J. Bibb Cain. Error-Correction Coding for Digital Communications. Applications of Communications Theory. New York: Plenum Press, 1981.
[2] Gitlin, Richard D., Jeremiah F. Hayes, and Stephen B. Weinstein. Data Communications Principles. Applications of Communications Theory. New York: Plenum Press, 1992.
[3] Heller, J., and I. Jacobs. “Viterbi Decoding for Satellite and Space Communication.” IEEE® Transactions on Communication Technology 19, no. 5 (October 1971): 835–48. https://doi.org/10.1109/TCOM.1971.1090711.
[4] Yasuda, Y., K. Kashiki, and Y. Hirata. “High-Rate Punctured Convolutional Codes for Soft Decision Viterbi Decoding.” IEEE Transactions on Communications 32, no. 3 (March 1984): 315–19. https://doi.org/10.1109/TCOM.1984.1096047.
[5] Haccoun, D., and G. Begin. “High-Rate Punctured Convolutional Codes for Viterbi and Sequential Decoding.” IEEE Transactions on Communications 37, no. 11 (November 1989): 1113–25. https://doi.org/10.1109/26.46505.
[6] Begin, G., D. Haccoun, and C. Paquin. “Further Results on High-Rate Punctured Convolutional Codes for Viterbi and Sequential Decoding.” IEEE Transactions on Communications 38, no. 11 (November 1990): 1922–28. https://doi.org/10.1109/26.61470.
[7] Moision, B. "A Truncation Depth Rule of Thumb for Convolutional Codes." In Information Theory and Applications Workshop (January 27 2008-February 1 2008, San Diego, California), 555-557. New York: IEEE, 2008.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Note
For decoding data encoded with truncated or terminated modes, or punctured codes, use the Viterbi Decoder (Wireless HDL Toolbox) block. The Wireless HDL Toolbox™ block provides an HDL-optimized algorithm with hardware-friendly control signals and simulates the latency of the HDL algorithm in Simulink.
HDL Coder provides additional configuration options that affect HDL implementation and synthesized logic.
HDL Coder supports the following features of the Viterbi Decoder block:
Non-recursive encoder/decoder with feed-forward trellis and simple shift register generation configuration
Continuous mode
Sample-based input
Decoder rates from 1/2 to 1/7
Constraint length from 3 to 9
When you set Decision type to Soft
decision, HDL code generation is supported for fixed-point input
and output data types. The input fixed-point data type must be
ufixN. N is the number of soft-decision
bits. HDL code generation is not supported for signed built-in data types
(int8, int16, int32).
When you set Decision type to Hard
decision, HDL code generation is supported for input with data
types ufix1 and Boolean. HDL code generation
is not supported for double and single input data types.
The Viterbi Decoder block decodes every bit by tracing back through a traceback depth that you define for the block. The block implements a complete traceback for each decision bit, using registers to store the minimum state index and branch decision in the traceback decoding unit. There are two methods to optimize the traceback logic: a pipelined register-based implementation or a RAM-based architecture. See the Generate HDL Code for Viterbi Decoder example.
You can specify that the traceback decoding unit be pipelined to improve the speed of the generated circuit. You can add pipeline registers to the traceback unit by specifying the number of traceback stages per pipeline register.
Using the TracebackStagesPerPipeline implementation
parameter, you can balance the circuit performance
based on system requirements. A smaller parameter value indicates the
requirement to add more registers to increase the speed of the traceback
circuit. Increasing the parameter value results in fewer registers along with a
decrease in the circuit speed.
Instead of using registers, you can choose to use RAMs to save the survivor branch information. The coder does not support Enable reset input port when using RAM-based traceback.
Right-click the block and open HDL Code > HDL Block Properties. Set the Architecture property to
RAM-based Traceback.Double-click the block and set the Traceback depth on the Viterbi Decoder block mask.
RAM-based traceback and register-based traceback differ in the following ways:
The RAM-based implementation traces back through one set of data to find the initial state to decode the previous set of data. The register-based implementation combines the traceback and decode operations into one step. It uses the best state found from the minimum operation as the decoding initial state.
RAM-based implementation traces back through M samples, decodes the previous M bits in reverse order, and releases one bit in order at each clock cycle. The register-based implementation decodes one bit after a complete traceback.
Because of the differences in the two traceback algorithms, the RAM-based implementation produces different numerical results than the register-based traceback. A longer traceback depth, for example, 10 times the constraint length, is recommended in the RAM-based traceback. This depth achieves a similar bit error rate (BER) as the register-based implementation. The size of RAM required for the implementation depends on the trellis and the traceback depth.
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| TracebackStagesPerPipeline |
Punctured code: Do not select this option. Punctured code requires frame-based input, which HDL Coder does not support.
Decision type: The coder does not support the
Unquantizeddecision type.Error if quantized input values are out of range: The coder does not support this option.
Operation mode: The coder supports only the
Continuousmode.Enable reset input port: When you enable both Enable reset input port and Delay reset action to next time step, HDL support is provided. You must select
Continuousoperation mode, and use register-based traceback.You cannot use the Viterbi Decoder block inside a Resettable Synchronous Subsystem (HDL Coder).
Version History
Introduced before R2006aUnquantized input values outside of the range [–1012, 1012] are clipped to –1012 and 1012, respectively.
See Also
Blocks
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
