Main Content

TuningGoal.Poles

Constraint on control system dynamics

expand all in page

Description

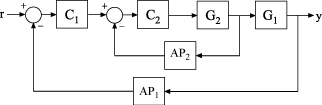
Use TuningGoal.Poles to constrain the closed-loop dynamics of a control system or of specific feedback loops within the control system. You can use this tuning goal for control system tuning with tuning commands, such as systune or looptune. A TuningGoal.Poles goal can ensure a minimum decay rate or minimum damping of the poles of the control system or loop. It can also eliminate fast dynamics in the tuned system.

Creation

Syntax

Req = TuningGoal.Poles(mindecay,mindamping,maxfreq)
Req = TuningGoal.Poles(location,mindecay,mindamping,maxfreq)

Description

Req = TuningGoal.Poles(mindecay,mindamping,maxfreq) creates a default template for constraining the closed-loop pole locations. The minimum decay rate, minimum damping constant, and maximum natural frequency define a region of the complex plane in which poles of the component must lie. Set mindecay = 0, mindamping = 0, or maxfreq = Inf to skip any of the three constraints.

example

Req = TuningGoal.Poles(location,mindecay,mindamping,maxfreq) constrains the poles of the sensitivity function measured at a specified location in the control system. (See getSensitivity (Simulink Control Design) for information about sensitivity functions.) Use this syntax to narrow the scope of the tuning goal to a particular feedback loop.

If you want to constrain the poles of the system with one or more feedback loops opened, set the Openings property. To limit the enforcement of this tuning goal to poles having natural frequency within a specified frequency range, set the Focus property. (See Properties.)

Input Arguments

expand all

Minimum decay rate of poles of tunable component, specified as a nonnegative scalar value in the frequency units of the control system model you are tuning.

When you tune the control system using this tuning goal, the closed-loop poles of the control system are constrained to satisfy:

  • Re(s) < -mindecay, for continuous-time systems.

  • log(|z|) < -mindecay*Ts, for discrete-time systems with sample time Ts.

Set mindecay = 0 to impose no constraint on the decay rate.

Desired minimum damping ratio of the closed-loop poles, specified as a value between 0 and 1.

Poles that depend on the tunable parameters are constrained to satisfy Re(s) < -mindamping*|s|. In discrete time, the damping ratio is computed using s=log(z)/Ts.

Set mindamping = 0 to impose no constraint on the damping ratio.

Desired maximum natural frequency of closed-loop poles, specified as a scalar value in the frequency units of the control system model you are tuning.

Poles are constrained to satisfy |s| < maxfreq for continuous time, or |log(z)| < maxfreq*Ts for discrete-time systems with sample time Ts. This constraint prevents fast dynamics in the closed-loop system.

Set maxfreq = Inf to impose no constraint on the natural frequency.

Location at which poles are assessed, specified as a character vector or cell array of character vectors that identify one or more locations in the control system to tune. When you use this input, the tuning goal constrains the poles of the sensitivity function measured at this location. (See getSensitivity (Simulink Control Design) for information about sensitivity functions.) What locations are available depends on what kind of system you are tuning:

  • If you are tuning a Simulink® model of a control system, you can use any linear analysis point marked in the model, or any linear analysis point in an slTuner (Simulink Control Design) interface associated with the Simulink model. Use addPoint (Simulink Control Design) to add analysis points to the slTuner interface. For example, if the slTuner interface contains an analysis point u, you can use 'u' to refer to that point when creating tuning goals. Use getPoints (Simulink Control Design) to get the list of analysis points available in an slTuner interface to your model.

  • If you are tuning a generalized state-space (genss) model of a control system, you can use any AnalysisPoint location in the control system model. For example, the following code creates a PI loop with an analysis point at the plant input 'u'. 

    AP = AnalysisPoint('u');
G = tf(1,[1 2]);
C = tunablePID('C','pi');
T = feedback(G*AP*C,1);

    When creating tuning goals, you can use 'u' to refer to the analysis point at the plant input. Use getPoints to get the list of analysis points available in a genss model.

If location specifies multiple locations, then the poles constraint applies to the sensitivity of the MIMO loop.

Properties

expand all

Minimum decay rate of closed-loop poles of tunable component, specified as a positive scalar value in the frequency units of the control system you are tuning. The initial value of this property is set by the mindecay input argument.

When you tune the control system using this tuning goal, closed-loop poles are constrained to satisfy Re(s) < -MinDecay for continuous-time systems, or log(|z|) < -MinDecay*Ts for discrete-time systems with sample time Ts.

You can use dot notation to change the value of this property after you create the tuning goal. For example, suppose Req is a TuningGoal.Poles tuning goal. Change the minimum decay rate to 0.001:

Req.MinDecay = 0.001;

Desired minimum damping ratio of closed-loop poles, specified as a value between 0 and 1. The initial value of this property is set by the mindamping input argument.

Poles that depend on the tunable parameters are constrained to satisfy Re(s) < -MinDamping*|s|. In discrete time, the damping ratio is computed using s=log(z)/Ts.

Desired maximum natural frequency of closed-loop poles, specified as a scalar value in the frequency units of the control system model you are tuning. The initial value of this property is set by the maxfreq input argument.

Poles of the block are constrained to satisfy |s| < maxfreq for continuous-time systems, or |log(z)| < maxfreq*Ts for discrete-time systems with sample time Ts. This constraint prevents fast dynamics in the tuned control system.

You can use dot notation to change the value of this property after you create the tuning goal. For example, suppose Req is a TuningGoal.ControllerPoles tuning goal. Change the maximum frequency to 1000:

Req.MaxFrequency = 1000;

Frequency band in which tuning goal is enforced, specified as a row vector of the form [min,max]. For continuous time, the default value is equal to [0,Inf]. For discrete time, the default value is equal to [0,pi/Ts], where Ts is the model sample time.

Set the Focus property to limit enforcement of the tuning goal to a particular frequency band. Express this value in the frequency units of the control system model you are tuning (rad/TimeUnit). For example, suppose Req is a tuning goal that you want to apply only between 1 and 100 rad/s. To restrict the tuning goal to this band, use the following command:

Req.Focus = [1,100];

Location at which poles are assessed, specified as a cell array of character vectors that identify one or more analysis points in the control system to tune. For example, if Location = {'u'}, the tuning goal evaluates the open-loop response measured at an analysis point 'u'. If Location = {'u1','u2'}, the tuning goal evaluates the MIMO open-loop response measured at analysis points 'u1' and 'u2'.

The initial value of the Location property is set by the location input argument when you create the tuning goal.

Models to which the tuning goal applies, specified as a vector of indices.

Use the Models property when tuning an array of control system models with systune, to enforce a tuning goal for a subset of models in the array. For example, suppose you want to apply the tuning goal, Req, to the second, third, and fourth models in a model array passed to systune. To restrict enforcement of the tuning goal, use the following command:

Req.Models = 2:4;

When Models = NaN, the tuning goal applies to all models.

Feedback loops to open when evaluating the tuning goal, specified as a cell array of character vectors that identify loop-opening locations. The tuning goal is evaluated against the open-loop configuration created by opening feedback loops at the locations you identify.

If you are using the tuning goal to tune a Simulink model of a control system, then Openings can include any linear analysis point marked in the model, or any linear analysis point in an slTuner (Simulink Control Design) interface associated with the Simulink model. Use addPoint (Simulink Control Design) to add analysis points and loop openings to the slTuner interface. Use getPoints (Simulink Control Design) to get the list of analysis points available in an slTuner interface to your model.

If you are using the tuning goal to tune a generalized state-space (genss) model of a control system, then Openings can include any AnalysisPoint location in the control system model. Use getPoints to get the list of analysis points available in the genss model.

For example, if Openings = {'u1','u2'}, then the tuning goal is evaluated with loops open at analysis points u1 and u2.

Name of the tuning goal, specified as a character vector.

For example, if Req is a tuning goal:

Req.Name = 'LoopReq';

Examples

collapse all

Open Live Script

Create a requirement that constrains the inner loop of the following control system to be stable and free of fast dynamics. Specify that the constraint is evaluated with the outer loop open.

Create a model of the system. To do so, specify and connect the numeric plant models, G1 and G2, and the tunable controllers C1 and C2. Also, create and connect the AnalysisPoint blocks, AP1 and AP2, which mark points of interest for analysis and tuning. 

G1 = tf(10,[1 10]);
G2 = tf([1 2],[1 0.2 10]);
C1 = tunablePID('C','pi');
C2 = tunableGain('G',1);
AP1 = AnalysisPoint('AP1');
AP2 = AnalysisPoint('AP2');
T = feedback(G1*feedback(G2*C2,AP2)*C1,AP1);

Create a tuning requirement that constrains the dynamics of the closed-loop poles. Restrict the poles of the inner loop to the region Re(s)<-0.1, |s|<30.

Req = TuningGoal.Poles(0.1,0,30);

Setting the minimum damping to zero imposes no constraint on the damping constants for the poles.

Specify that the constraint on the tuned system poles is applied with the outer loop open.

Req.Openings = 'AP1';

When you tune T using this requirement, the constraint applies to the poles of the entire control system evaluated with the loop open at 'AP1'. In other words, the poles of the inner loop plus the poles of C1 and G1 are all considered.

After you tune T, you can use viewGoal to validate the tuned control system against the requirement.

Open Live Script

Create a requirement that constrains the inner loop of the system of the previous example to be stable and free of fast dynamics. Specify that the constraint is evaluated with the outer loop open.

Create a tuning requirement that constrains the dynamics of the inner feedback loop, the loop identified by AP2. Restrict the poles of the inner loop to the region Re(s)<-0.1, |s|<30.

Req = TuningGoal.Poles('AP2',0.1,0,30);

Specify that the constraint on the tuned system poles is applied with the outer loop open. 

Req.Openings = 'AP1';

When you tune T using this requirement, the constraint applies only to the poles of the inner loop, evaluated with the outer loop open. In this case, since G1 and C1 do not contribute to the sensitivity function at AP2 when the outer loop is open, the requirement constrains only the poles of G2 and C2.

After you tune T, you can use viewGoal to validate the tuned control system against the requirement.

Tips

  • TuningGoal.Poles restricts the closed-loop dynamics of the tuned control system. To constrain the dynamics or ensure the stability of a single tunable component, use TuningGoal.ControllerPoles.

Algorithms

When you tune a control system using a TuningGoal, the software converts the tuning goal into a normalized scalar value f(x). x is the vector of free (tunable) parameters in the control system. The software then adjusts the parameter values to minimize f(x), or to drive f(x) below 1 if the tuning goal is a hard constraint.

For TuningGoal.Poles, f(x) reflects the relative satisfaction or violation of the goal. For example, if you attempt to constrain the closed-loop poles of a feedback loop to a minimum damping of ζ = 0.5, then:

  • f(x) = 1 means the smallest damping among the constrained poles is ζ = 0.5 exactly.

  • f(x) = 1.1 means the smallest damping ζ = 0.5/1.1 = 0.45, roughly 10% less than the target.

  • f(x) = 0.9 means the smallest damping ζ = 0.5/0.9 = 0.55, roughly 10% better than the target.

Version History

Introduced in R2016a

expand all

See Also

| | (Simulink Control Design) | (Simulink Control Design) | | | | |

Topics