Passivity Indices
This example shows how to compute various measures of passivity for linear time-invariant systems.
Passive Systems
A linear system G(s) is passive when all I/O trajectories satisfy
where denotes the transpose of .

To measure "how passive" a system is, we use passivity indices.
The input passivity index is defined as the largest such that
The system G is "input strictly passive" (ISP) when . is also called the "input feedforward passivity" (IFP) index and corresponds to the minimum feedforward action needed to make the system passive.
The output passivity index is defined as the largest such that
The system G is "output strictly passive" (OSP) when . is also called the "output feedback passivity" (OFP) index and corresponds to the minimum feedback action needed to make the system passive.
The I/O passivity index is defined as the largest such that
The system is "very strictly passive" (VSP) if .
Circuit Example
Consider the following example. We take the current as the input and the voltage as the output. Based on Kirchhoff's current and voltage law, we obtain the transfer function for ,

Let , and .
R = 2; L = 1; C = 0.1;
s = tf('s');
G = (L*s+R)*(R*s+1/C)/(L*s^2 + 2*R*s+1/C);Use isPassive to check whether is passive.
PF = isPassive(G)
PF = logical
1
Since PF = true, is passive. Use getPassiveIndex to compute the passivity indices of .
% Input passivity index nu = getPassiveIndex(G,'in')
nu = 2
% Output passivity index rho = getPassiveIndex(G,'out')
rho = 0.2857
% I/O passivity index tau = getPassiveIndex(G,'io')
tau = 0.2642
Since , the system is very strictly passive.
Frequency-Domain Characterization
A linear system is passive if and only if it is "positive real":
The smallest eigenvalue of the left-hand-side is related to the input passivity index :
where denotes the smallest eigenvalue. Similarly, when is minimum-phase, the output passivity index is given by:
Verify this for the circuit example. Plot the Nyquist plot of the circuit transfer function.
nyquist(G)
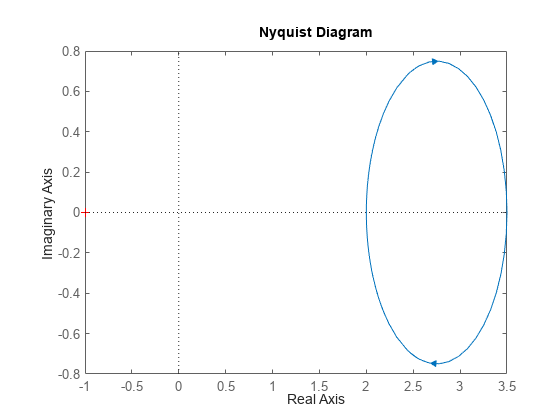
The entire Nyquist plot lies in the right-half plane so is positive real. The leftmost point on the Nyquist curve is so the input passivity index is , the same value we obtained earlier. Similarly, the leftmost point on the Nyquist curve for gives the output passivity index value .
Relative Passivity Index
It can be shown that the "positive real" condition
is equivalent to the small gain condition
The relative passivity index (R-index) is the peak gain over frequency of when is minimum phase, and otherwise:
In the time domain, the R-index is the smallest such that
.
The system is passive if and only if , and the smaller is, the more passive the system is. Use getPassiveIndex to compute the R-index for the circuit example.
R = getPassiveIndex(G)
R = 0.5556
The resulting value indicates that the circuit is a very passive system.
References
[1] Xia, M., P. Gahinet, N. Abroug, C. Buhr, and E. Laroche. “Sector Bounds in Stability Analysis and Control Design.” International Journal of Robust and Nonlinear Control 30, no. 18 (December 2020): 7857–82. https://doi.org/10.1002/rnc.5236.