Series Interconnection of Passive Systems
This example illustrates the properties of a series interconnection of passive systems.
Series Interconnection of Passive Systems
Consider an interconnection of two subsystems and in series. The interconnected system is given by the mapping from input to output .
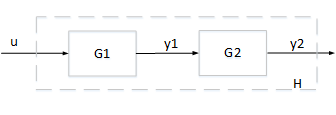
In contrast with parallel and feedback interconnections, passivity of the subsystems and does not guarantee passivity for the interconnected system . Take for example
Both systems are passive as confirmed by
G1 = tf([5 3 1],[1,2,1]); isPassive(G1)
ans = logical
1
G2 = tf([1,1,5,.1],[1,2,3,4]); isPassive(G2)
ans = logical
1
However the series interconnection of and is not passive:
H = G2*G1; isPassive(H)
ans = logical
0
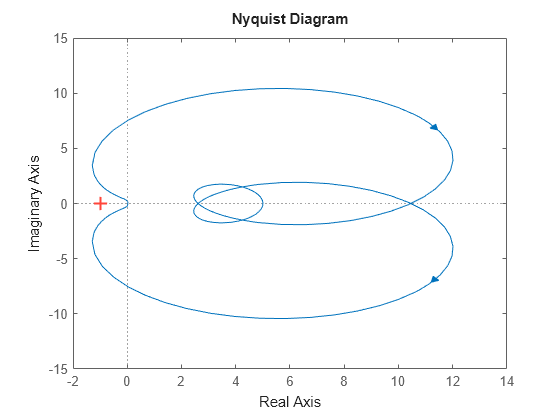
This is confirmed by verifying that the Nyquist plot of is not positive real.
nyquist(H)
Passivity Indices for Series Interconnection
While the series interconnection of passive systems is not passive in general, there is a relationship between the passivity indices of and and the passivity indices of . Let and denote the input passivity indices for and , and let and denote the output passivity indices. If all these indices are positive, then the input passivity index and the output passivity index for the series interconnection satisfy
In other words, the shortage of passivity at the inputs or outputs of is no worse than the right-hand-side expressions. For details, see the paper by Arcak, M. and Sontag, E.D., "Diagonal stability of a class of cyclic systems and its connection with the secant criterion," Automatica, Vol 42, No. 9, 2006, pp. 1531-1537. Verify these lower bounds for the example above.
% Output passivity index for G1 rho1 = getPassiveIndex(G1,'output'); % Output passivity index for G2 rho2 = getPassiveIndex(G2,'output'); % Input passivity index for H=G2*G1 nu = getPassiveIndex(H,'input')
nu = -1.2886
% Lower bound
-0.125/(rho1*rho2)ans = -2.4194
Similarly, verify the lower bound for the output passivity index of .
% Input passivity index for G1 nu1 = getPassiveIndex(G1,'input'); % Input passivity index for G2 nu2 = getPassiveIndex(G2,'input'); % Output passivity index for H=G2*G1 rho = getPassiveIndex(H,'output')
rho = -0.6966
% Lower bound
-0.125/(nu1*nu2)ans = -6.0000