Plot Impulse Response of Regression Model with ARIMA Errors
Impulse response functions help examine the effects of a unit
innovation shock to future values of the response of a time series model, without
accounting for the effects of exogenous predictors. For example, if an innovation shock
to an aggregate output series, e.g., GDP, is persistent, then GDP is sensitive to such
shocks. The examples below show how to plot impulse response functions for regression
models with various ARIMA error model structures using impulse.
Regression Model with AR Errors
This example shows how to plot the impulse response function for a regression model with AR errors.
Specify the regression model with AR(4) errors:
Mdl = regARIMA('Intercept',2,'Beta',[5; -1],'AR',... {0.9, -0.8, 0.75, -0.6})
Mdl =
regARIMA with properties:
Description: "Regression with ARMA(4,0) Error Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
Intercept: 2
Beta: [5 -1]
P: 4
Q: 0
AR: {0.9 -0.8 0.75 -0.6} at lags [1 2 3 4]
SAR: {}
MA: {}
SMA: {}
Variance: NaN
The dynamic multipliers are absolutely summable because the autoregressive component is stable. Therefore, Mdl is stationary.
You do not need to specify the innovation variance.
Plot the impulse response function.
impulse(Mdl)

The impulse response decays to 0 since Mdl defines a stationary error process. The regression component does not impact the impulse responses.
Regression Model with MA Errors
This example shows how to plot a regression model with MA errors.
Specify the regression model with MA(10) errors:
Mdl = regARIMA('Intercept',2,'Beta',[5; -1],... 'MA',{0.5,-0.4,-0.3,0.2,-0.1},'MALags',[2 4 6 8 10])
Mdl =
regARIMA with properties:
Description: "Regression with ARMA(0,10) Error Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
Intercept: 2
Beta: [5 -1]
P: 0
Q: 10
AR: {}
SAR: {}
MA: {0.5 -0.4 -0.3 0.2 -0.1} at lags [2 4 6 8 10]
SMA: {}
Variance: NaN
The dynamic multipliers are absolutely summable because the moving average component is invertible. Therefore, Mdl is stationary.
You do not need to specify the innovation variance.
Plot the impulse response function for 10 responses.
impulse(Mdl,10)
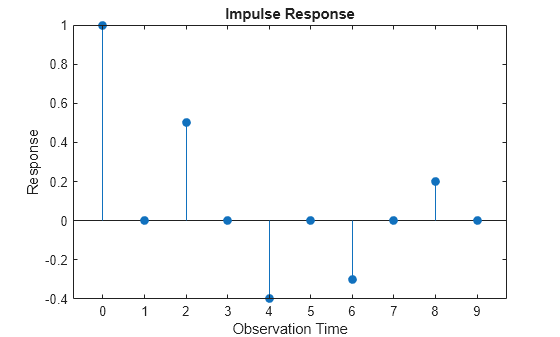
The impulse response of an MA error model is simply the MA coefficients at their corresponding lags.
Regression Model with ARMA Errors
This example shows how to plot the impulse response function of a regression model with ARMA errors.
Specify the regression model with ARMA(4,10) errors:
Mdl = regARIMA('Intercept',2,'Beta',[5; -1],... 'AR',{0.9, -0.8, 0.75, -0.6},... 'MA',{0.5, -0.4, -0.3, 0.2, -0.1},'MALags',[2 4 6 8 10])
Mdl =
regARIMA with properties:
Description: "Regression with ARMA(4,10) Error Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
Intercept: 2
Beta: [5 -1]
P: 4
Q: 10
AR: {0.9 -0.8 0.75 -0.6} at lags [1 2 3 4]
SAR: {}
MA: {0.5 -0.4 -0.3 0.2 -0.1} at lags [2 4 6 8 10]
SMA: {}
Variance: NaN
The dynamic multipliers are absolutely summable because the autoregressive component is stable, and the moving average component is invertible. Therefore, Mdl defines a stationary error process.
You do not need to specify the innovation variance.
Plot the first 30 impulse responses.
impulse(Mdl,30)

The impulse response decays to 0 since Mdl defines a stationary error process.
Regression Model with ARIMA Errors
This example shows how to plot the impulse response function of a regression model with ARIMA errors.
Specify the regression model with ARIMA(4,1,10) errors:
Mdl = regARIMA('Intercept',2,'Beta',[5; -1],... 'AR',{0.9, -0.8, 0.75, -0.6},... 'MA',{0.5, -0.4, -0.3, 0.2, -0.1},... 'MALags',[2 4 6 8 10],'D',1)
Mdl =
regARIMA with properties:
Description: "Regression with ARIMA(4,1,10) Error Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
Intercept: 2
Beta: [5 -1]
P: 5
D: 1
Q: 10
AR: {0.9 -0.8 0.75 -0.6} at lags [1 2 3 4]
SAR: {}
MA: {0.5 -0.4 -0.3 0.2 -0.1} at lags [2 4 6 8 10]
SMA: {}
Variance: NaN
One of the roots of the compound autoregressive polynomial is 1, therefore Mdl defines a nonstationary error process.
You do not need to specify the innovation variance.
Plot the first impulse responses.
quot = sum([1,cell2mat(Mdl.MA)])/sum([1,-cell2mat(Mdl.AR)])
quot = 1.2000
impulse(Mdl,50) hold on plot([1 50],[quot quot],'r--','Linewidth',2.5) hold off

The impulse responses do not decay to 0. They settle at the quotient of the sums of the moving average and autoregressive polynomial coefficients (quot).