Pressure Compensator
(To be removed) Valve used to regulate the pressure drop across a hydraulic component
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Libraries:
Simscape /
Fluids /
Hydraulics (Isothermal) /
Valves /
Pressure Control Valves
Description
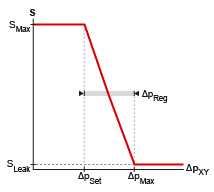
The Pressure Compensator block models the flow through a valve that constricts so as to maintain a preset pressure drop between a chosen two hydraulic nodes. The valve has four hydraulic ports, two being flow passages (the inlet, A, and the outlet, B) and two pressure sensors (X and Y). The normally open valve contracts when the pressure drop from X to Y rises above the valve pressure setting. The drop in opening area is a function of the pressure drop—proportional to it in a linear parameterization (the block default) or a general function of it in a tabulated parameterization. The valve serves its purpose until it hits the limit of its pressure regulation range—a point at which the valve is fully closed and the pressure drop can again rise unabated.
Valve Opening
The opening area calculation depends on the valve parameterization selected for
the block: either Linear area-opening relationship or
Tabulated data - Area vs. pressure.
If the Valve parameterization block parameter is in the
default setting of Linear area-opening relationship,
the opening area is computed as:
where:
SMax is the value specified in the Maximum passage area block parameter.
ΔpSet is the value specified in the Valve pressure setting block parameter.
ΔpXY is the pressure drop from port X to port Y:
where p is the gauge pressure at the port indicated by the subscript (X or Y).
k is the linear constant of proportionality:
where in turn:
SLeak is the value specified in the Leakage area block parameter.
ΔpReg is that specified in the Valve regulation range block parameter.
At and below the valve pressure setting, the opening area is that of a fully open valve:
At and above a maximum pressure, the opening area is that due to internal leakage alone:
where the maximum pressure drop ΔpMax is the sum:
Opening area in the Linear area-opening
relationship parameterization
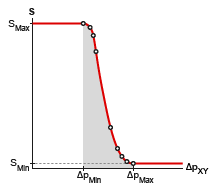
If the Valve parameterization block parameter is set to
Tabulated data - Area vs. pressure, the opening
area is computed as:
where SXY is a tabulated function constructed from the Pressure drop vector and Opening area vector block parameters. The function is based on linear interpolation (for points within the data range) and nearest-neighbor extrapolation (for points outside the data range). The leakage and maximum opening areas are the minimum and maximum values of the Valve opening area vector block parameter.
Opening area in the Tabulated data - Area vs.
pressure parameterization
By default, the valve opening dynamics are ignored. The valve is assumed to
respond instantaneously to changes in the pressure drop, without time lag
between the onset of a pressure disturbance and the increased valve opening that
the disturbance produces. If such time lags are of consequence in a model, you
can capture them by setting the Opening dynamics block
parameter to Include valve opening dynamics. The
valves then open each at a rate given by the expression:
where τ is a measure of the time needed
for the instantaneous opening area (subscript In) to reach a
new steady-state value (subscript SS).
The primary purpose of the leakage area of a closed valve is to ensure that at no time does a portion of the hydraulic network become isolated from the remainder of the model. Such isolated portions reduce the numerical robustness of the model and can slow down simulation or cause it to fail. Leakage is generally present in minuscule amounts in real valves but in a model its exact value is less important than it being a small number greater than zero. The leakage area is obtained from the block parameter of the same name.
Valve Flow Rate
The causes of the pressure losses incurred in the passages of the valve are ignored in the block. Whatever their natures—sudden area changes, flow passage contortions—only their cumulative effect is considered during simulation. This effect is captured in the block by the discharge coefficient, a measure of the flow rate through the valve relative to the theoretical value that it would have in an ideal valve. The flow rate through the valve is defined as:
where:
q is the volumetric flow rate through the valve.
CD is the value of the Flow discharge coefficient block parameter.
S is the opening area of the valve.
ΔpAB is the pressure drop from port A to port B.
pCrit is the pressure differential at which the flow shifts between the laminar and turbulent flow regimes.
The calculation of the critical pressure depends on the setting of the
Laminar transition specification block parameter. If this
parameter is in the default setting of By pressure ratio:
where:
pAtm is the atmospheric pressure (as defined for the corresponding hydraulic network).
pAvg is the average of the gauge pressures at ports A and B.
βCrit is the value of the Laminar flow pressure ratio block parameter.
If the Laminar transition specification block parameter is
instead set to By Reynolds number:
where:
ReCrit is the value of the Critical Reynolds number block parameter.
ν is the kinematic viscosity specified for the hydraulic network.
DH is the instantaneous hydraulic diameter: