Calculate the Frequency Response of a 2-D Filter

This example shows how to calculate and display the frequency response of a two-dimensional filter using the freqz2 function. The frequency response of a filter describes the gain of a filter at different input frequencies.

With no output arguments, freqz2 creates a mesh plot of the frequency response. For example, consider this FIR filter.

h = [0.1667    0.6667    0.1667
     0.6667   -3.3333    0.6667
     0.1667    0.6667    0.1667];

Calculate and display the 64-by-64 point frequency response of h.

freqz2(h)

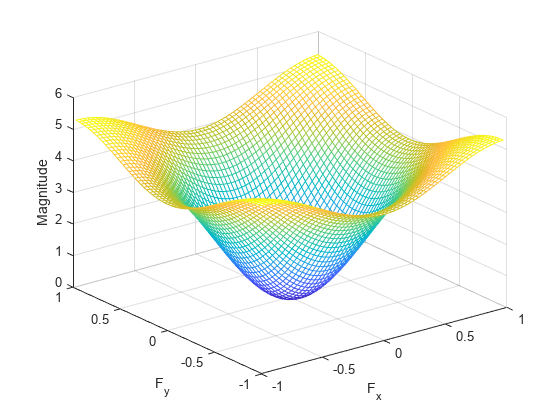
To obtain the frequency response H and the frequency point vectors f1 and f2, use output arguments.

[H,f1,f2] = freqz2(h);

freqz2 normalizes the frequencies f1 and f2 so that the value 1.0 corresponds to half the sampling frequency, or π radians.

For a simple m-by-n response, as shown above, freqz2 uses the two-dimensional fast Fourier transform function fft2. You can also specify vectors of arbitrary frequency points, but in this case freqz2 uses a slower algorithm.