Fan-Beam Projection
Note
For information about creating projection data from line integrals along parallel
paths, see Radon Transform. To
convert fan-beam projection data to parallel-beam projection data, use the fan2para function.
The fanbeam function computes
projections of an image matrix along specified directions. A
projection of a two-dimensional function f(x,y) is a set of line
integrals. The fanbeam function computes the line integrals along
paths that radiate from a single source, forming a fan shape. To represent an image, the
fanbeam function takes multiple projections of the image from
different angles by rotating the source around the center of the image. The following
figure shows a single fan-beam projection at a specified rotation angle.
Fan-Beam Projection at Rotation Angle Theta

When you compute fan-beam projection data using the fanbeam
function, you specify as arguments an image and the distance between the vertex of the
fan-beam projections and the center of rotation (the center pixel in the image). The
fanbeam function determines the number of beams, based on the
size of the image and the values of specified name-value arguments.
The FanSensorGeometry name-value argument specifies how sensors are
aligned: "arc" or "line".
| Fan Sensor Geometry | Description |
|---|---|
"arc" | fanbeam positions the sensors along an arc,
spacing the sensors at 1 degree intervals. Use the
FanSensorSpacing parameter to control the
distance between sensors by specifying the angle between each beam. This
is the default fan sensor geometry. |
"line" | fanbeam positions sensors along a straight line,
rather than an arc. Use the FanSensorSpacing
parameter to specify the distance between the sensors, in pixels, along
the x´ axis. |
The FanRotationIncrement parameter specifies the rotation angle
increment. By default, fanbeam takes projections at different
angles by rotating the source around the center pixel at 1 degree intervals.
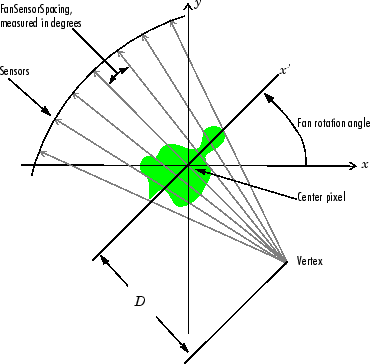
The following figures illustrate both these geometries. The first figure illustrates
geometry used by the fanbeam function when
FanSensorGeometry is set to "arc" (the
default). Note how you specify the distance between sensors by specifying the angular
spacing of the beams.
Fan-Beam Projection with Arc Geometry
The following figure illustrates the geometry used by the fanbeam
function when FanSensorGeometry is set to "line".
In this figure, note how you specify the position of the sensors by specifying the
distance between them in pixels along the x´ axis.
Fan-Beam Projection with Line Geometry

Image Reconstruction from Fan-Beam Projection Data
To reconstruct an image from fan-beam projection data, use the
ifanbeam function. With this function, you specify as
arguments the projection data and the distance between the vertex of the fan-beam
projections and the center of rotation when the projection data was created. For
example, this code recreates the image I from the projection data
P and distance D.
I = ifanbeam(P,D);
By default, the ifanbeam function assumes that the fan-beam
projection data was created using the arc fan sensor geometry, with beams spaced at
1 degree angles and projections taken at 1 degree increments over a full 360 degree
range. As with the fanbeam function, you can use
ifanbeam name-value arguments to specify other values for
these characteristics of the projection data. Use the same values for these
name-value arguments that were used when the projection data was created. For more
information about these parameters, see ifanbeam.
The ifanbeam function converts the fan-beam projection data
to parallel-beam projection data with the fan2para function,
and then calls the iradon function to perform the image
reconstruction. For this reason, the ifanbeam function supports
certain iradon parameters, which it passes to the
iradon function. See The Inverse Radon Transformation for more information about the
iradon function.
Reconstruct Image Using Inverse Fanbeam Projection
This example shows how to use fanbeam and ifanbeam to form projections from a sample image and then reconstruct the image from the projections.
Create a test image of the Shepp-Logan head phantom using the phantom function. The phantom image illustrates many of the qualities that are found in real-world tomographic imaging of human heads.
P = phantom(256); imshow(P)

Compute fan-beam projection data of the test image, using the FanSensorSpacing name-value argument to vary the sensor spacing. The example uses the fanbeam arc geometry, so you specify the spacing between sensors by specifying the angular spacing of the beams. The first call spaces the beams at 2 degrees; the second at 1 degree; and the third at 0.25 degrees. In each call, the distance between the center of rotation and vertex of the projections is constant at 250 pixels. In addition, fanbeam rotates the projection around the center pixel at 1 degree increments.
D = 250; dsensor1 = 2; F1 = fanbeam(P,D,"FanSensorSpacing",dsensor1); dsensor2 = 1; F2 = fanbeam(P,D,"FanSensorSpacing",dsensor2); dsensor3 = 0.25; [F3,sensor_pos3,rot_angles3] = fanbeam(P,D,"FanSensorSpacing",dsensor3);
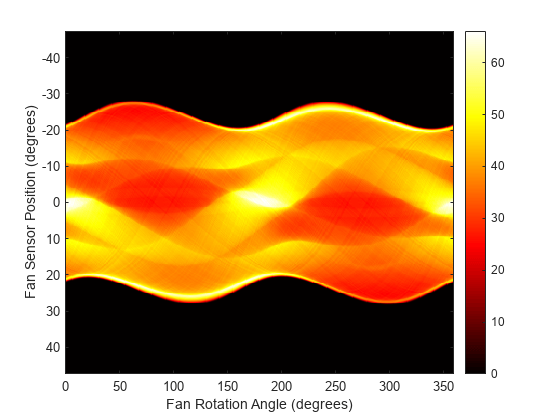
Plot the projection data F3. Because fanbeam calculates projection data at rotation angles from 0 to 360 degrees, the same patterns occur at an offset of 180 degrees. The same features are being sampled from both sides.
figure imagesc(rot_angles3,sensor_pos3,F3) colormap(hot); colorbar xlabel("Fan Rotation Angle (degrees)") ylabel("Fan Sensor Position (degrees)")
Reconstruct the image from the fan-beam projection data using ifanbeam. In each reconstruction, match the fan sensor spacing with the spacing used when the projection data was created previously. The example uses the OutputSize name-value argument to constrain the output size of each reconstruction to be the same as the size of the original image P. In the output, note how the quality of the reconstruction gets better as the number of beams in the projection increases. The first image, Ifan1, was created using 2 degree spacing of the beams; the second image, Ifan2, was created using 1 degree spacing of the beams; the third image, Ifan3, was created using 0.25 spacing of the beams.
output_size = max(size(P)); Ifan1 = ifanbeam(F1,D, ... "FanSensorSpacing",dsensor1,"OutputSize",output_size); figure, imshow(Ifan1) title("Ifan1")

Ifan2 = ifanbeam(F2,D, ... "FanSensorSpacing",dsensor2,"OutputSize",output_size); figure, imshow(Ifan2) title("Ifan2")

Ifan3 = ifanbeam(F3,D, ... "FanSensorSpacing",dsensor3,"OutputSize",output_size); figure, imshow(Ifan3) title("Ifan3")
