cart2pol
Transform Cartesian coordinates to polar or cylindrical
Description
Examples
Input Arguments
Output Arguments
Algorithms
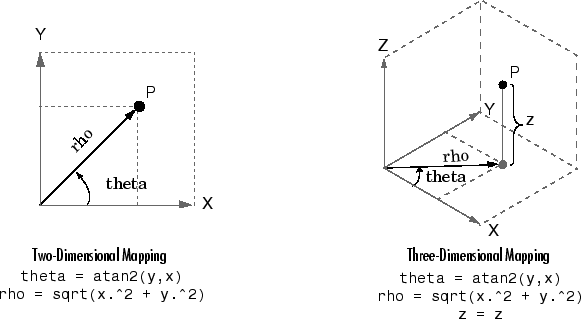
The mapping from two-dimensional Cartesian coordinates to polar coordinates, and from three-dimensional Cartesian coordinates to cylindrical coordinates is
Extended Capabilities
Version History
Introduced before R2006a