nufft

Nonuniform fast Fourier transform

Since R2020a

Syntax

Y = nufft(X,t)

Y = nufft(X,t,f)

Y = nufft(X,t,f,dim)

Y = nufft(X)

Description

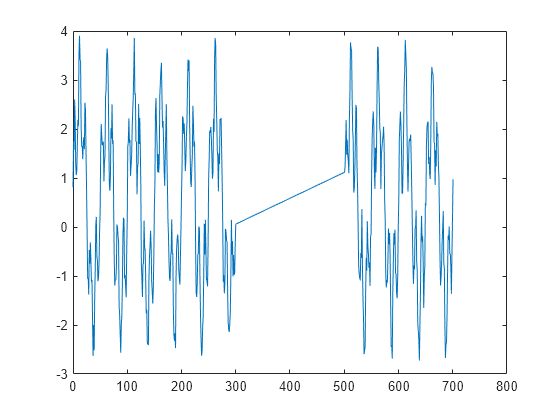
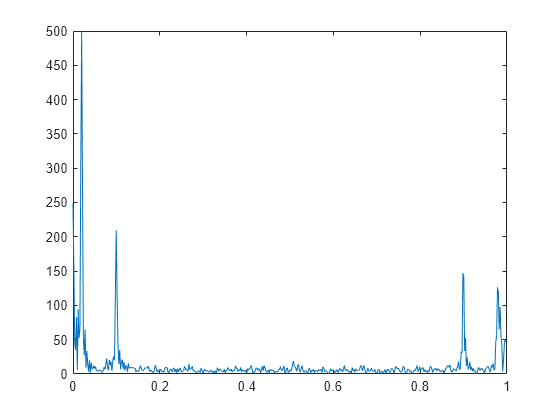
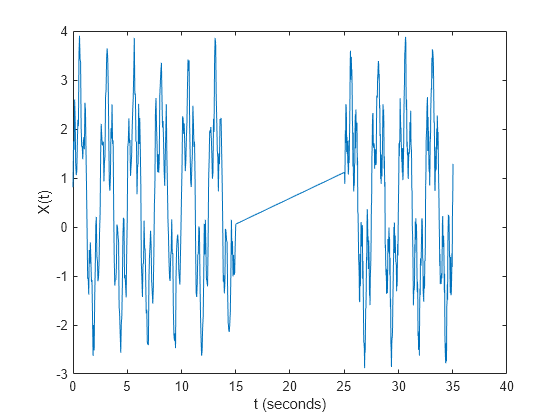
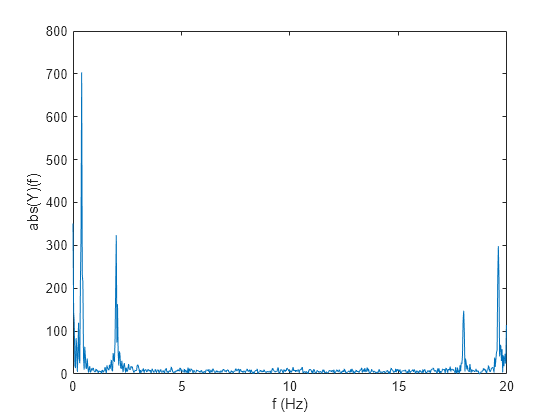
Y = nufft(X,t) returns the nonuniform discrete Fourier transform (NUDFT) of X using the sample points t.

• If X is a vector, then nufft returns the transform of the vector.

• If X is a matrix, then nufft treats the columns of X as vectors and returns the transform of each column.

• If X is a multidimensional array, then nufft treats the values along the first array dimension whose size does not equal 1 as vectors and returns the transform of each vector.

Y = nufft(X,t,f) computes the NUDFT at the query points f using the sample points t. To specify f without specifying sample points, use nufft(X,[],f).

Y = nufft(X,t,f,dim) returns the NUDFT along dimension dim. For example, nufft(X,t,f,2) computes the transform of each row of a matrix X.

Y = nufft(X) returns the discrete Fourier transform of X, and is equivalent to fft(X).

Examples

Nonuniform Sample Points With Default Frequencies

Create a signal X sampled at unevenly spaced points t. Plot the signal.

t = [0:300 500.5:700.5];
S = 2*sin(2*pi*0.02*t) + sin(2*pi*0.1*t);
X = S + rand(size(t));
plot(t,X)

Find the nonuniform fast Fourier transform of the signal. When you use nufft without providing the frequencies as the third argument, nufft uses the default frequency scaling where the frequencies take the form f(i) = (i-1)/n for a signal length of n. Plot the absolute value of the transform as a function of the default frequencies.

Y = nufft(X,t);
n = length(t);
f = (0:n-1)/n;
plot(f,abs(Y))

Nonuniform Sample Points With Time and Frequency Scaling

Create a time vector of nonuniform sampled points. Define a time duration of about 35 seconds with a sampling period T = 50 ms (or a sampling frequency Fs = 20 Hz) for the equivalent uniformly sampled data.

T = 50e-3;    % Sampling period of 50 ms for equivalent uniform samples
Fs = 1/T;     % Sampling frequency of 20 Hz for equivalent uniform samples
t = [0:T:300*T 500.5*T:T/2:700.5*T];

Create a signal X sampled at unevenly spaced points t with peak frequencies at 0.4 Hz and 2 Hz.

S = 2*sin(2*pi*0.4*t) + sin(2*pi*2*t);    % Signal with peak frequencies at 0.4 Hz and 2 Hz
X = S + rand(size(t));
plot(t,X)
xlabel("t (seconds)")
ylabel("X(t)")

Find the nonuniform fast Fourier transform of the signal. Use nufft without providing the frequencies as the third argument. In this case, nufft uses the default frequencies with the form f(i) = (i-1)/n for a signal length of n. The nonuniform discrete Fourier transform treats the nonuniform sample points t and frequencies f as if they have a sampling period of 1 s and a sampling frequency of 1 Hz for the equivalent uniformly sampled data. For this reason, include the scaling factor T to the time vector when using nufft to obtain the transform with correctly scaled units. Plot the absolute value of the transform as a function of the default frequencies that are scaled by Fs.

Y = nufft(X,t/T);
n = length(t);
f = (0:n-1)/n*Fs;
plot(f,abs(Y))
xlabel("f (Hz)")
ylabel("abs(Y)(f)")

When using nufft, you can also specify a nonuniform frequency vector or query points f as the third argument and the nonuniform time vector t as the second argument. Here, you do not need to rescale t and f when using nufft. Plot the absolute value of the transform as a function of the nonuniform frequencies.

f = [0:0.5:n/4 n/3+1:n-120]/n*Fs;
Y = nufft(X,t,f);
plot(f,abs(Y))
xlabel("f (Hz)")
ylabel("abs(Y)(f)")

Frequencies of Musical Chord

Define and label the frequencies of a range of musical tones.

C3 = 440 / (2^(21/12));
nOctaves = 3;
musicalTones = C3 * 2.^((0:(12*nOctaves-1))/12);
toneNames = ["C";"C#";"D";"D#";"E";"F";"F#";"G";"G#";"A";"A#";"B"] + string(3:(3+nOctaves-1));
toneNames = categorical(toneNames, toneNames);

Define the audio signal sampling frequency in Hz, the sample points n, and a signal containing a major chord X.

fs = 16e3;
n = 1:16000;
X = 4*cos(2*pi*(440/fs)*n) + 2*cos(2*pi*(554.37/fs)*n) + 3*cos(2*pi*(659.2/fs)*n);

Compute and plot the frequency components of the major chord.

Y = nufft(X,[],musicalTones/fs);
bar(toneNames(:),abs(Y))

Input Arguments

X — Input array

vector | matrix | multidimensional array

Input array, specified as a vector, matrix, or multidimensional array.

Data Types: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
Complex Number Support: Yes

t — Sample points or time vector

0:(n-1) (default) | vector

Sample points or time vector, specified as a vector of length n, where n is the length of the operating dimension of the input array X. By default, the sample points vector is 0:(n-1).

When you use the default sample points 0:(n-1), nufft treats t and f as if they have a sampling period of 1 s and a sampling frequency of 1 Hz for the equivalent uniformly sampled data. For this reason, you might need to rescale your time and frequency vectors to obtain the Fourier transform with correctly scaled units. For example, see Nonuniform Sample Points With Time and Frequency Scaling.

Data Types: double | single

f — Query points or frequency vector

0:(n-1)/n (default) | vector

Query points or frequency vector, specified as a vector. By default, the query points vector is (0:(n-1))/n, where n is the length of the operating dimension of the input array X. To specify f without specifying sample points, use nufft(X,[],f).

When you use the default query points (0:(n-1))/n, nufft treats t and f as if they have a sampling period of 1 s and a sampling frequency of 1 Hz for the equivalent uniformly sampled data. For this reason, you might need to rescale your time and frequency vectors to obtain the Fourier transform with correctly scaled units. For example, see Nonuniform Sample Points With Time and Frequency Scaling.

Data Types: double | single

dim — Dimension to operate along

positive integer scalar

Dimension to operate along, specified as a positive integer scalar. The default is the first array dimension whose size does not equal 1.

Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical

More About

Nonuniform Discrete Fourier Transform of Vector

For a vector X of length n, sample points t, and frequencies f, the nonuniform discrete Fourier transform of X is defined as

$$Y(k)={\displaystyle \sum _{j=1}^{n}X(j)e^{-2\pi it(j)f(k)}}$$

where k = 1, 2, …, m. When t = 0, 1, …, n-1 and f = (0, 1, …, n-1)/n (defaults for nufft), the formula is equivalent to the uniform discrete Fourier transform used by the fft function.

References

[1] Potter, Samuel F., Nail A. Gumerov, and Ramani Duraiswami. “Fast Interpolation of Bandlimited Functions.” In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 4516–20. New Orleans, LA: IEEE, 2017. https://doi.org/10.1109/ICASSP.2017.7953011.

[2] Dutt, A., and V. Rokhlin. “Fast Fourier Transforms for Nonequispaced Data.” SIAM Journal on Scientific Computing 14, no. 6 (November 1993): 1368–93. https://doi.org/10.1137/0914081.

Extended Capabilities

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

Version History

Introduced in R2020a