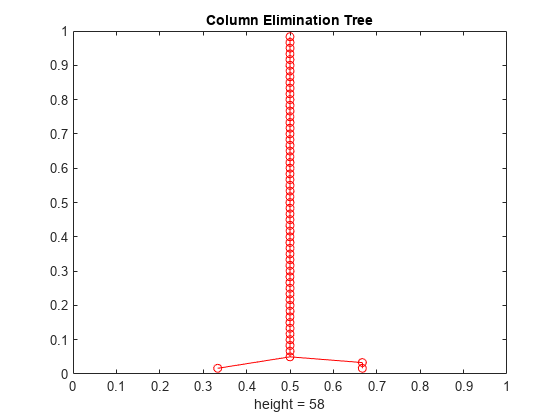
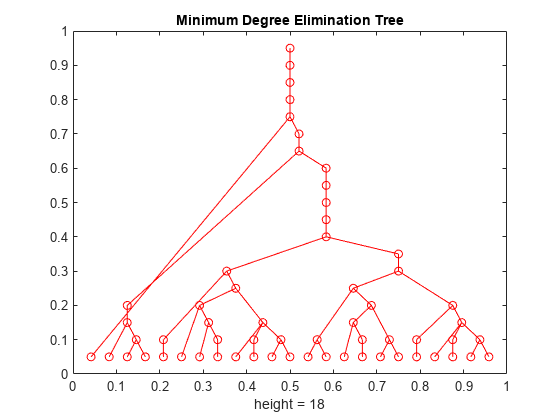
etree
Elimination tree
Description
Examples
Input Arguments
Output Arguments
More About
References
[1] Chen, Yanqing, Timothy A. Davis, William W. Hager, and Sivasankaran Rajamanickam. “Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate.” ACM Transactions on Mathematical Software 35, no. 3 (October 2008): 1–14. https://doi.org/10.1145/1391989.1391995.
[2] Pothen, Alex, and Sivan Toledo. "Elimination Structures in Scientific Computing." In Handbook of Data Structures and Applications, edited by Dinesh P. Mehta and Sartaj Sahni, 945–965. New York: Chapman and Hall/CRC, 2017. https://doi.org/10.1201/9781315119335
Extended Capabilities
Version History
Introduced before R2006aSee Also
chol | treelayout | etreeplot | treeplot