inpolygon
Points located inside or on edge of polygonal region
Description
Examples
Define a pentagon and a set of points. Then, determine which points lie inside (or on the edge) of the pentagon.
Define the x and y coordinates of polygon vertices to create a pentagon.
L = linspace(0,2*pi,6); xv = cos(L)'; yv = sin(L)';
Define x and y coordinates of 250 random query points. Initialize the random-number generator to make the output of randn repeatable.
rng default
xq = randn(250,1);
yq = randn(250,1);Determine whether each point lies inside or on the edge of the polygon area. Also determine whether any of the points lie on the edge of the polygon area.
[in,on] = inpolygon(xq,yq,xv,yv);
Determine the number of points lying inside or on the edge of the polygon area.
numel(xq(in))
ans = 80
Determine the number of points lying on the edge of the polygon area.
numel(xq(on))
ans = 0
Since there are no points lying on the edge of the polygon area, all 80 points identified by xq(in), yq(in) are strictly inside the polygon area.
Determine the number of points lying outside the polygon area (not inside or on the edge).
numel(xq(~in))
ans = 170
Plot the polygon and the query points. Display the points inside the polygon with a red plus. Display the points outside the polygon with a blue circle.
figure plot(xv,yv) % polygon axis equal hold on plot(xq(in),yq(in),'r+') % points inside plot(xq(~in),yq(~in),'bo') % points outside hold off

Find the points inside a square with a square hole.
Define a square region with a square hole. Specify the vertices of the outer loop in a counterclockwise direction, and specify the vertices for the inner loop in a clockwise direction. Use NaN to separate the coordinates for the outer and inner loops.
xv = [1 4 4 1 1 NaN 2 2 3 3 2]; yv = [1 1 4 4 1 NaN 2 3 3 2 2];
Define x and y coordinates of 500 random points. Initialize the random-number generator to make the output of randn repeatable.
rng default
xq = rand(500,1)*5;
yq = rand(500,1)*5;Determine whether each point lies inside or on the edge of the polygon area.
in = inpolygon(xq,yq,xv,yv);
Plot the polygon and the query points. Display the points inside the polygon with a red plus. Display the points outside the polygon with a blue circle.
figure plot(xv,yv,'LineWidth',2) % polygon axis equal hold on plot(xq(in),yq(in),'r+') % points inside plot(xq(~in),yq(~in),'bo') % points outside hold off

Query points in the square hole are outside the polygon.
Define the x and y coordinates for a pentagram.
xv = [0.5;0.2;1.0;0;0.8;0.5]; yv = [1.0;0.1;0.7;0.7;0.1;1];
Define the x and y coordinates of 12 query points.
xq = [0.1;0.5;0.9;0.2;0.4;0.5;0.5;0.9;0.6;0.8;0.7;0.2]; yq = [0.4;0.6;0.9;0.7;0.3;0.8;0.2;0.4;0.4;0.6;0.2;0.6];
Determine whether each point lies inside or on the edge of the polygon area. Also determine whether any of the points lie on the edge of the polygon area.
[in,on] = inpolygon(xq,yq,xv,yv);
Determine the number of points lying inside or on the edge of the polygon area.
numel(xq(in))
ans = 8
Determine the number of points lying on the edge of the polygon area.
numel(xq(on))
ans = 2
Determine the number of points lying outside the polygon area (not inside or on the edge).
numel(xq(~in))
ans = 4
Plot the polygon and the points. Display the points strictly inside the polygon with a red plus. Display the points on the edge with a black asterisk. Display the points outside the polygon with a blue circle.
figure plot(xv,yv) % polygon hold on plot(xq(in&~on),yq(in&~on),'r+') % points strictly inside plot(xq(on),yq(on),'k*') % points on edge plot(xq(~in),yq(~in),'bo') % points outside hold off
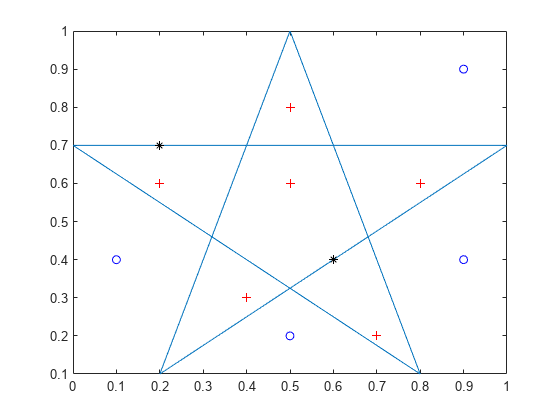
Six points lie inside the polygon. Two points lie on the edge of the polygon. Four points lie outside the polygon.
Input Arguments
x-coordinates of query points, specified as a scalar, vector, matrix, or multidimensional array.
The size of xq must match the size of yq.
Data Types: double | single
y-coordinates of query points, specified as a scalar, vector, matrix, or multidimensional array.
The size of yq must match the size of xq.
Data Types: double | single
x-coordinates of polygon vertices, specified as a vector.
The size of xv must match the size of yv.
To specify vertices of multiply connected or disjoint polygons,
separate the coordinates for distinct loops with NaN.
Additionally for multiply connected polygons, you must orient the
vertices for external and internal loops in opposite directions.
The polygon cannot be self-intersecting and multiply connected due to the ambiguity associated with self-intersections and loop orientations.
Data Types: double | single
y-coordinates of polygon vertices, specified as a vector.
The size of yv must match the size of xv.
To specify vertices of multiply connected or disjoint polygons,
separate the coordinates for distinct loops with NaN.
Additionally for multiply connected polygons, you must orient the
vertices for external and internal loops in opposite directions.
The polygon cannot be self-intersecting and multiply connected due to the ambiguity associated with self-intersections and loop orientations.
Data Types: double | single
Output Arguments
Indicator for the points inside or on the edge of the polygon
area, returned as a logical array. in is the same
size as xq and yq.
A logical
1(true) indicates that the corresponding query point is inside the polygonal region or on the edge of the polygon boundary.A logical
0(false) indicates that the corresponding query point is outside the polygonal region.
Therefore, you can use in to index into xq and yq to
identify query points of interest.
xq(in), yq(in) | Query points inside or on the edge of the polygon area |
xq(~in), yq(~in) | Query points outside the polygonal region |
Indicator for the points on the edge of the polygon area, returned
as a logical array. on is the same size as xq and yq.
A logical
1(true) indicates that the corresponding query point is on the polygon boundary.A logical
0(false) indicates that the corresponding query point is inside or outside the polygon boundary.
Therefore, you can use on and in to
index into xq and yq identify
query points of interest.
xq(on), yq(on) | Query points on the polygon boundary |
xq(~on), yq(~on) | Query points inside or outside the polygon boundary |
xq(in&~on), yq(in&~on) | Query points strictly inside the polygonal region |
Extended Capabilities
Usage notes and limitations:
Supports single-precision and double-precision inputs, but uses double-precision arithmetic even if all inputs are single-precision.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The inpolygon function
fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)