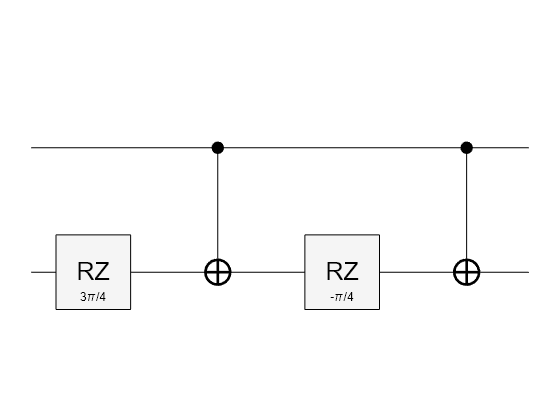
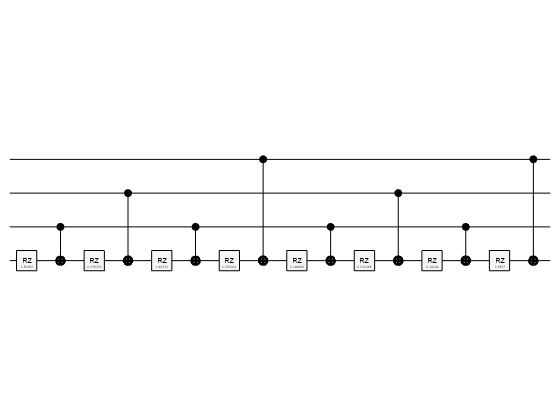
ucrzGate
Installation Required: This functionality requires MATLAB Support Package for Quantum Computing.
Syntax
Description
cg = ucrzGate(controlQubits,targetQubit,theta)theta to a
single target qubit for each computational basis state of the control qubits.
cg = ucrzGate(controlQubits,targetQubit,theta,RotationThreshold=thresh)
Examples
Input Arguments
Output Arguments
More About
References
[1] Möttönen, Mikko, Juha J. Vartiainen, Ville Bergholm, and Martti M. Salomaa. "Quantum Circuits for General Multiqubit Gates." Physical Review Letters 93, no. 13 (September 20, 2004): 130502. https://doi.org/10.1103/PhysRevLett.93.130502.
[2] Camps, Daan, and Roel Van Beeumen. "FABLE: Fast Approximate Quantum Circuits for Block-Encodings." In 2022 IEEE International Conference on Quantum Computing and Engineering (QCE), 104–113. Broomfield, CO, USA: IEEE, 2022. https://doi.org/10.1109/QCE53715.2022.00029.
Version History
Introduced in R2023b