Occupancy Grids
Overview
Occupancy grids are used to represent a robot workspace as a discrete grid. Information about the environment can be collected from sensors in real time or be loaded from prior knowledge. Laser range finders, bump sensors, cameras, and depth sensors are commonly used to find obstacles in your robot’s environment.
Occupancy grids are used in robotics algorithms such as path planning (see mobileRobotPRM (Robotics System Toolbox) or plannerRRT).
They are used in mapping applications for integrating sensor information in a discrete
map, in path planning for finding collision-free paths, and for localizing robots in a
known environment (see monteCarloLocalization or matchScans). You can create maps with different sizes and resolutions to
fit your specific application.
For 3-D occupancy maps, see occupancyMap3D.
For 2-D occupancy grids, there are two representations:
Binary occupancy grid (see
binaryOccupancyMap)Probability occupancy grid (see
occupancyMap)
A binary occupancy grid uses true values
to represent the occupied workspace (obstacles) and false values
to represent the free workspace. This grid shows where obstacles are
and whether a robot can move through that space. Use a binary occupancy
grid if memory size is a factor in your application.
A probability occupancy grid uses probability values to create a more detailed map representation. This representation is the preferred method for using occupancy grids. This grid is commonly referred to as simply an occupancy grid. Each cell in the occupancy grid has a value representing the probability of the occupancy of that cell. Values close to 1 represent a high certainty that the cell contains an obstacle. Values close to 0 represent certainty that the cell is not occupied and obstacle free. The probabilistic values can give better fidelity of objects and improve performance of certain algorithm applications.
Binary and probability occupancy grids share several properties and algorithm details. Grid and world coordinates apply to both types of occupancy grids. The inflation function also applies to both grids, but each grid implements it differently. The effects of the log-odds representation and probability saturation apply to probability occupancy grids only.
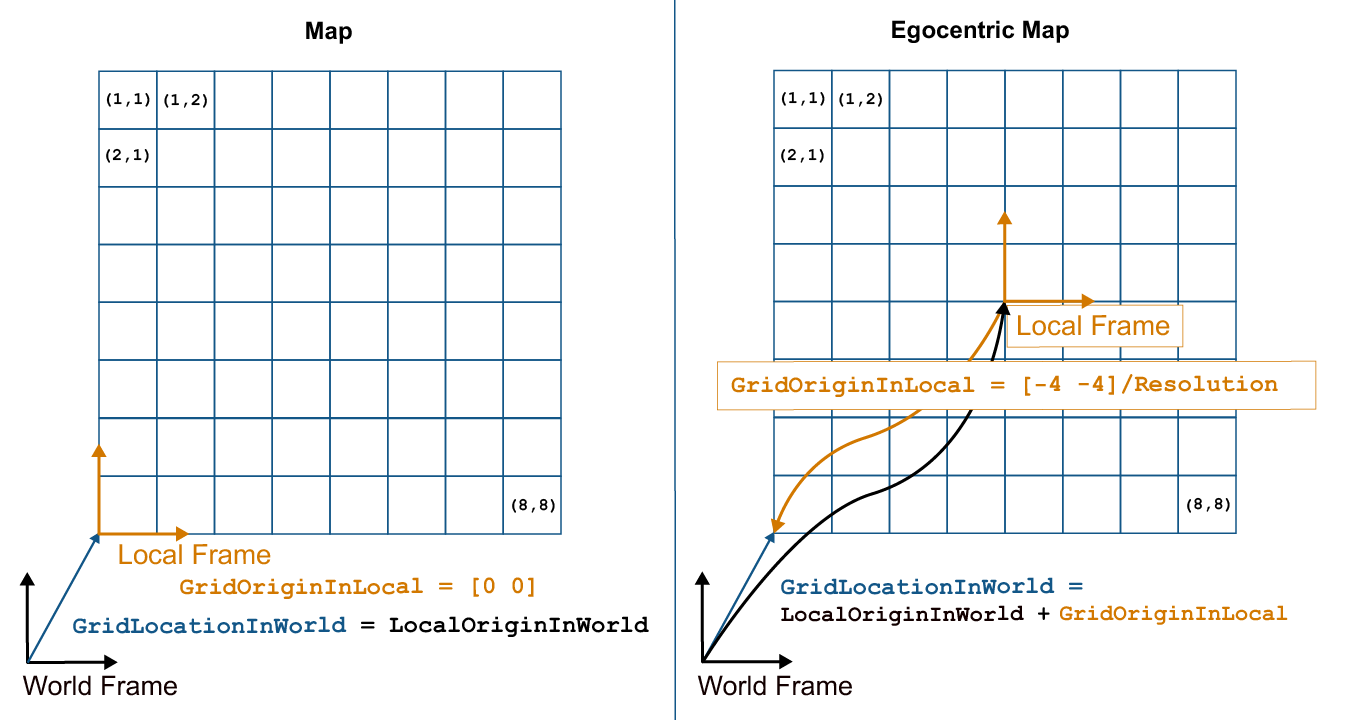
World, Grid, and Local Coordinates
When working with occupancy grids in MATLAB®, you can use either world, local, or grid coordinates.
The absolute reference frame in which the robot operates is referred to as the world frame in the occupancy grid. Most operations are performed in the world frame, and it is the default selection when using MATLAB functions in this toolbox. World coordinates are used as an absolute coordinate frame with a fixed origin, and points can be specified with any resolution. However, all locations are converted to grid locations because of data storage and resolution limits on the map itself.
The local frame refers to the egocentric frame for a vehicle
navigating the map. The GridOriginInLocal and
LocalOriginInWorld properties define the origin of the grid in
local coordinates and the relative location of the local frame in the world coordinates.
You can adjust this local frame using the move function. For an example using the local frame as
an egocentric map to emulate a vehicle moving around and sending local obstacles, see
Create Egocentric Occupancy Maps Using Range Sensors.
Grid coordinates define the actual resolution of the occupancy
grid and the finite locations of obstacles. The origin of grid coordinates
is in the top-left corner of the grid, with the first location having
an index of (1,1). However, the GridLocationInWorld property
of the occupancy grid in MATLAB defines the bottom-left corner
of the grid in world coordinates. When creating an occupancy grid
object, properties such as XWorldLimits and YWorldLimits are
defined by the input width, height,
and resolution. This figure shows a visual representation
of these properties and the relation between world and grid coordinates.
Inflation of Coordinates
Both the binary and normal occupancy grids have an option for inflating obstacles. This
inflation is used to add a factor of safety on obstacles and create buffer zones between
the robot and obstacle in the environment. The inflate function of an
occupancy grid object converts the specified radius to the number of
cells rounded up from the resolution*radius value. Each algorithm
uses this cell value separately to modify values around obstacles.
Binary Occupancy Grid
The inflate function
takes each occupied cell and directly inflates it by adding occupied space around
each point. This basic inflation example illustrates how the radius value is
used.
Inflate Obstacles in a Binary Occupancy Grid
This example shows how to create the map, set the obstacle locations and inflate it by a radius of 1m. Extra plots on the figure help illustrate the inflation and shifting due to conversion to grid locations.
Create binary occupancy grid. Set occupancy of position [5,5].
map = binaryOccupancyMap(10,10,5); setOccupancy(map,[5 5], 1);
Inflate occupied spaces on map by 1m.
inflate(map,1); show(map)
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains an object of type image.](../../examples/nav_robotics/win64/InflateObstaclesInABinaryOccupancyGridExample_01.png)
Plot original location, converted grid position and draw the original circle. You can see from this plot, that the grid center is [4.9 4.9], which is shifted from the [5 5] location. A 1m circle is drawn from there and notice that any cells that touch this circle are marked as occupied. The figure is zoomed in to the relevant area.
hold on theta = linspace(0,2*pi); x = 4.9+cos(theta); % x circle coordinates y = 4.9+sin(theta); % y circle coordinates plot(5,5,'*b','MarkerSize',10) % Original location plot(4.9,4.9,'xr','MarkerSize',10) % Grid location center plot(x,y,'-r','LineWidth',2); % Circle of radius 1m. axis([3.6 6 3.6 6]) ax = gca; ax.XTick = [3.6:0.2:6]; ax.YTick = [3.6:0.2:6]; grid on legend('Original Location','Grid Center','Inflation')
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 4 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Original Location, Grid Center, Inflation.](../../examples/nav_robotics/win64/InflateObstaclesInABinaryOccupancyGridExample_02.png)
As you can see from the above figure, even cells that barely overlap with the inflation radius are labeled as occupied.
Occupancy Grids
The inflate function uses the inflation
radius to perform probabilistic inflation. Probabilistic
inflation acts as a local maximum operator and finds the highest probability values
for nearby cells. The inflate function uses this definition to
inflate the higher probability values throughout the grid. This inflation increases
the size of any occupied locations and creates a buffer zone for robots to navigate
around obstacles. This example shows how the inflation works with a range of
probability values.
Inflate Obstacles in an Occupancy Grid
This example shows how the inflate method performs probabilistic inflation on obstacles to inflate their size and create a buffer zone for areas with a higher probability of obstacles.
Create a 10m x 10m empty map.
map = occupancyMap(10,10,10);
Update occupancy of world locations with specific values in pvalues.
x = [1.2; 2.3; 3.4; 4.5; 5.6]; y = [5.0; 4.0; 3.0; 2.0; 1.0]; pvalues = [0.2 0.4 0.6 0.8 1]; updateOccupancy(map,[x y],pvalues) figure show(map)
![Figure contains an axes object. The axes object with title Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains an object of type image.](../../examples/nav/win64/InflateObstaclesInAnOccupancyGridExample_01.png)
Inflate occupied areas by a given radius. Larger occupancy values are written over smaller values. You can copy your map beforehand to revert any unwanted changes.
savedMap = copy(map); inflate(map,0.5) figure show(map)
![Figure contains an axes object. The axes object with title Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains an object of type image.](../../examples/nav/win64/InflateObstaclesInAnOccupancyGridExample_02.png)
Log-Odds Representation of Probability Values
When using occupancy grids with probability values, the goal is to estimate the
probability of obstacle locations for use in real-time robotics applications. The
occupancyMap class uses a log-odds
representation of the probability values for each cell. Each probability value is
converted to a corresponding log-odds value for internal storage. The value is converted
back to probability when accessed. This representation efficiently updates probability
values with the fewest operations. Therefore, you can quickly integrate sensor data into
the map.
The log-odds representation uses the following equation:
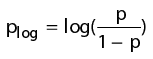
Note
Log-odds values are stored as int16 values. This data type
limits the resolution of probability values to ±0.001 but greatly improves
memory size and allows for creation of larger maps.
Probability Saturation
When updating an occupancy grid with observations using the log-odds representation, the values have a range of –∞ to ∞. This range means if a robot observes a location such as a closed door multiple times, the log-odds value for this location becomes unnecessarily high, or the value probability gets saturated. If the door then opens, the robot needs to observe the door open many times before the probability changes from occupied to free. In dynamic environments, you want the map to react to changes to more accurately track dynamic objects.
To prevent this saturation, update the ProbabilitySaturation
property, which limits the minimum and maximum probability values allowed when
incorporating multiple observations. This property is an upper and lower bound on
the log-odds values and enables the map to update quickly to changes in the
environment. The default minimum and maximum values of the saturation limits are
[0.001 0.999]. For dynamic environments, the suggested values
are at least [0.12 0.97]. Consider modifying this range if the
map does not update rapidly enough for multiple observations.
See Also
binaryOccupancyMap | occupancyMap | occupancyMap3D