Gaussian Antenna as Approximation for Spiral Antenna
This example shows how a Gaussian antenna can approximate the radiation pattern of a spiral antenna. Spiral antennas are known for their wideband behavior and are often used in wideband communications. The Gaussian antenna approximation is widely used in the literature.
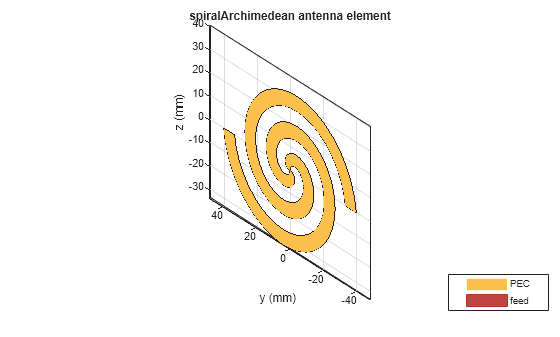
Create a spiral antenna using Antenna Toolbox™. The antenna is in the y-z plane and has inner and outer radii of 0.65 mm and 40 mm, respectively.
se = spiralArchimedean( ... InnerRadius=0.65e-3,OuterRadius=40e-3, ... Tilt=90,TiltAxis="y"); show(se)
Compute the radiation pattern for the spiral antenna at an operating frequency of 4 GHz. Specify a range of azimuth angles from –90° to 90° and zero elevation. Normalize the pattern so that its maximum value is 0 dB.
fc = 4e9; az = -90:0.5:90; sePattern = pattern(se,fc,az,0, ... CoordinateSystem="rectangular",Type="powerdb"); sePatternNorm = sePattern - max(sePattern);
Use Phased Array System Toolbox™ to create a Gaussian element with the same beamwidth as the spiral antenna. Compute its radiation pattern, which is normalized by construction.
seBw = beamwidth(se,fc,az,0); ge = phased.GaussianAntennaElement(Beamwidth=seBw); gePattern = pattern(ge,fc,az,0, ... CoordinateSystem="rectangular",Type="powerdb");
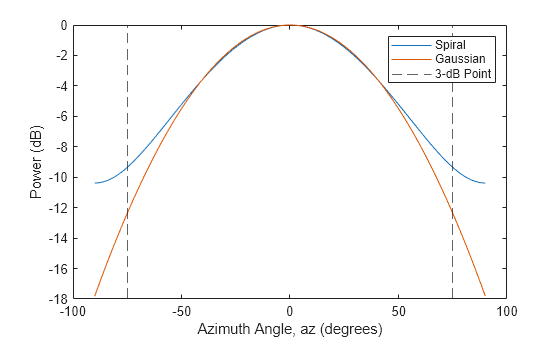
Find the smallest positive azimuth angle at which the patterns differ by about 3 dB.
idx = find((abs(sePatternNorm.' - gePattern) >= 3) & (az' >= 0),1); az3dB = az(idx);
Plot the patterns for the spiral and Gaussian antennas. Overlay the 3-dB points. The Gaussian antenna pattern matches the spiral antenna pattern well out to about 75 degrees and thus can be used as an excellent approximation of a spiral antenna.
plot(az,sePatternNorm,az,gePattern) xline([-az3dB az3dB],'--') xlabel("Azimuth Angle, az (degrees)") ylabel("Power (dB)") legend("Spiral","Gaussian","3-dB Point")
See Also
phased.GaussianAntennaElement | spiralArchimedean (Antenna Toolbox)