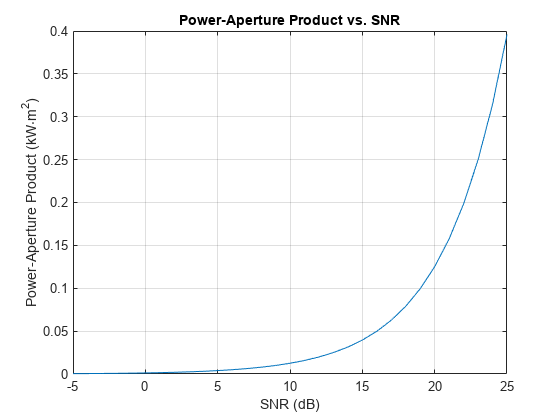
radareqsearchpap
Description
pap = radareqsearchpap(___,Name,Value)'Loss',6 specifies system losses
as 6 decibels.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Barton, David Knox. Radar Equations for Modern Radar. Artech House Radar Series. Boston, Mass: Artech House, 2013.
[2] Skolnik, Merrill I. Introduction to Radar Systems. Third edition. McGraw-Hill Electrical Engineering Series. Boston, Mass. Burr Ridge, IL Dubuque, IA: McGraw Hill, 2001.
Extended Capabilities
Version History
Introduced in R2021a