Train DQN Agent for Lane Keeping Assist
This example shows how to train a deep Q-learning network (DQN) agent for lane keeping assist (LKA) in Simulink®. For more information on DQN agents, see Deep Q-Network (DQN) Agent.
Fix Random Number Stream for Reproducibility
The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility. Fix the random number stream with seed 0 and random number algorithm Mersenne twister. For more information on controlling the seed used for random number generation, see rng.
previousRngState = rng(0,"twister");The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.
Simulink Model for the Ego Car
The reinforcement learning environment for this example is a simple bicycle model for the ego vehicle dynamics. The training goal is to keep the ego vehicle traveling along the centerline of the lanes by adjusting the front steering angle. This example uses the same vehicle model as in Lane Keeping Assist System Using Model Predictive Control (Model Predictive Control Toolbox). The ego car dynamics is specified by the following parameters.
m = 1575; % total vehicle mass (kg) Iz = 2875; % yaw moment of inertia (mNs^2) lf = 1.2; % longitudinal distance from CG to front tires (m) lr = 1.6; % longitudinal distance from CG to rear tires (m) Cf = 19000; % cornering stiffness of front tires (N/rad) Cr = 33000; % cornering stiffness of rear tires (N/rad) Vx = 15; % longitudinal velocity (m/s)
Define the sample time Ts and simulation duration Tf in seconds.
Ts = 0.1; T = 15;
The output of the LKA system is the front steering angle of the ego car. To simulate the physical limitations of the ego car, constrain the steering angle to the range [-0.5,0.5] rad.
u_min = -0.5; u_max = 0.5;
The curvature of the road is defined by a constant 0.001 (). The initial value for the lateral deviation is 0.2 m and the initial value for the relative yaw angle is –0.1 rad.
rho = 0.001; e1_initial = 0.2; e2_initial = -0.1;
Open the model.
mdl = "rlLKAMdl"; open_system(mdl); agentblk = mdl + "/RL Agent";
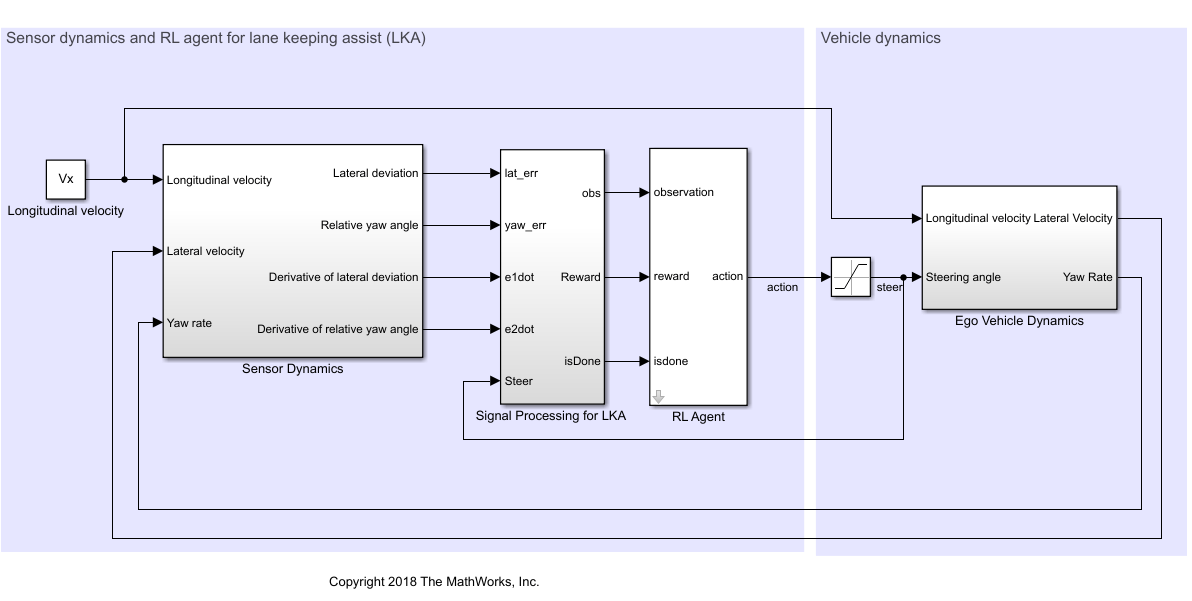
In this model:
The steering-angle action signal from the agent to the environment is from –15 degrees to 15 degrees.
The observations from the environment are the lateral deviation , the relative yaw angle , their derivatives and , and their integrals and .
The simulation is terminated when the lateral deviation
The reward , provided at every time step , is
where is the control input from the previous time step .
Create Environment Interface
Create a reinforcement learning environment object for the ego vehicle. To do so, first create the observation and action specifications.
observationInfo = rlNumericSpec([6 1], ... LowerLimit=-inf*ones(6,1), ... UpperLimit=inf*ones(6,1)); observationInfo.Name = "observations"; observationInfo.Description = ... "Lateral deviation and relative yaw angle"; actionInfo = rlFiniteSetSpec((-15:15)*pi/180); actionInfo.Name = "steering";
Then, create the environment object.
env = rlSimulinkEnv(mdl,agentblk,observationInfo,actionInfo);
The object has a discrete action space where the agent can apply one of 31 possible steering angles from –15 degrees to 15 degrees. The observation is the six-dimensional vector containing lateral deviation, relative yaw angle, as well as their derivatives and integrals with respect to time.
To define the initial condition for lateral deviation and relative yaw angle, specify an environment reset function using an anonymous function handle. This reset function randomizes the initial values for the lateral deviation and relative yaw angle.
env.ResetFcn = @(in)localResetFcn(in);
Create DQN agent
DQN agents use a parametrized Q-value function approximator to estimate the value of the policy.
Since DQN agents have a discrete action space, you have the option to create a vector (that is multi-output) Q-value function critic, which is generally more efficient than a comparable single-output critic.
A discrete vector Q-value function takes only the observation as input and returns as output a single vector with as many elements as the number of possible discrete actions. The value of each output element represents the expected discounted cumulative long-term reward for taking the action corresponding to the element number, from the state corresponding to the current observation, and following the policy afterwards.
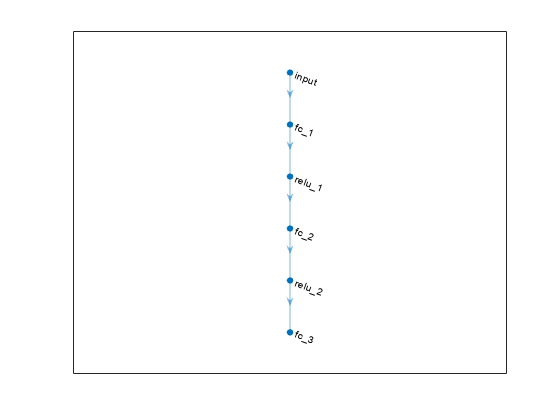
To model the parametrized Q-value function within the critic, use a deep neural network with one input (the six-dimensional observed state) and one output vector with 31 elements (evenly spaced steering angles from -15 to 15 degrees).
% Define number of inputs, neurons, and outputs nI = observationInfo.Dimension(1); % number of inputs (6) nL = 24; % number of neurons nO = numel(actionInfo.Elements); % number of outputs (31) % Define network as array of layer objects dnn = [ featureInputLayer(nI) fullyConnectedLayer(nL) reluLayer fullyConnectedLayer(nL) reluLayer fullyConnectedLayer(nO) ]; % Convert to dlnetwork object dnn = dlnetwork(dnn);
Display the number of parameters and view the network configuration.
summary(dnn)
Initialized: true
Number of learnables: 1.5k
Inputs:
1 'input' 6 features
plot(dnn)
Create the critic using dnn and the observation and action specifications. For more information, see rlQValueFunction.
critic = rlVectorQValueFunction(dnn,observationInfo,actionInfo);
Specify training options for the critic using rlOptimizerOptions.
criticOptions = rlOptimizerOptions( ... LearnRate=1e-3, ... GradientThreshold=1, ... L2RegularizationFactor=1e-4);
Specify the DQN agent options using rlDQNAgentOptions, include the training options for the critic.
agentOptions = rlDQNAgentOptions(... SampleTime=Ts,... UseDoubleDQN=true,... CriticOptimizerOptions=criticOptions,... ExperienceBufferLength=1e6,... MiniBatchSize=64); agentOptions.EpsilonGreedyExploration.EpsilonDecay = 1e-4;
Then, create the DQN agent using the specified critic representation and agent options. For more information, see rlDQNAgent.
agent = rlDQNAgent(critic,agentOptions);
Train Agent
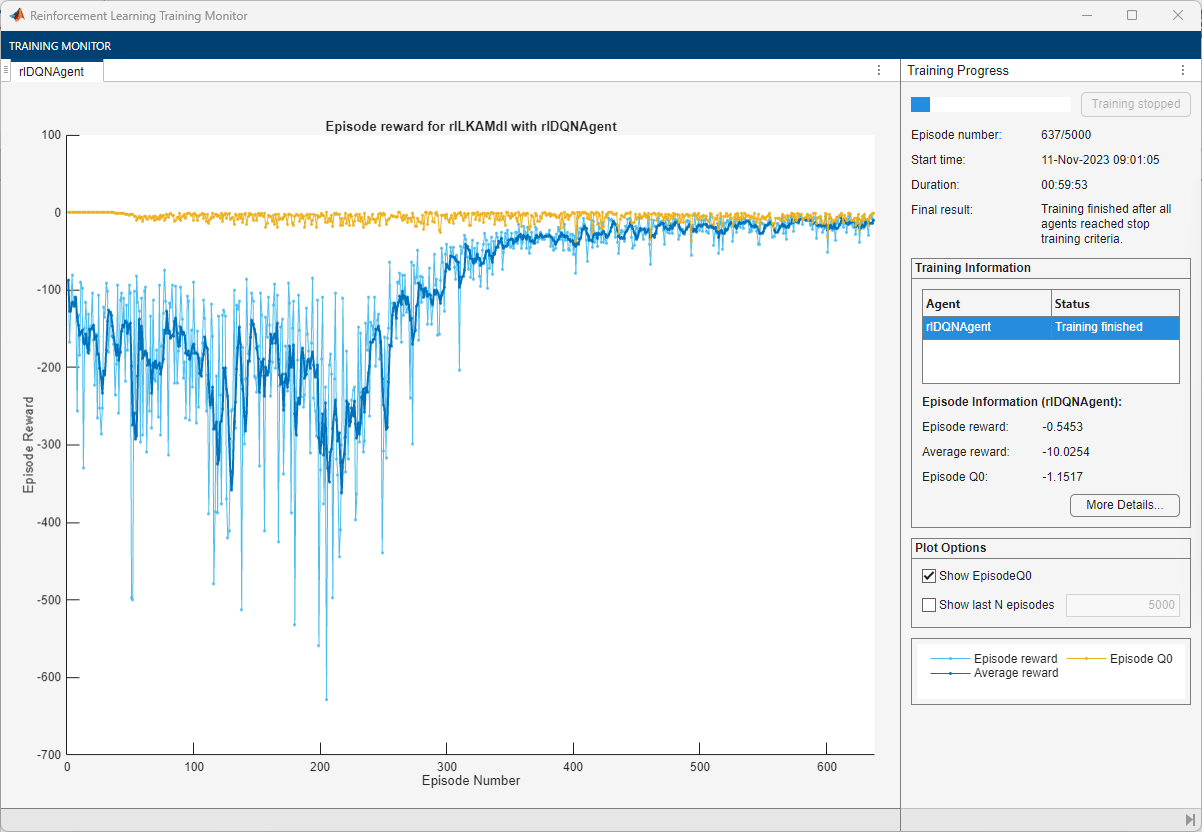
To train the agent, first specify the training options. For this example, use the following options:
Run each training episode for a maximum of 5000 episodes, with each episode lasting at most
ceil(T/Ts)time steps.Display the training progress in the Reinforcement Learning Training Monitor dialog box (set the
Plotsoption totraining-progress) and disable the command line display (set theVerboseoption tofalse).Stop training when the episode reward reaches
–1.Save a copy of the agent for each episode where the cumulative reward is greater than
–2.5.
For more information on training options, see rlTrainingOptions.
maxepisodes = 5000; maxsteps = ceil(T/Ts); trainingOpts = rlTrainingOptions(... MaxEpisodes=maxepisodes,... MaxStepsPerEpisode=maxsteps,... Verbose=false,... Plots="training-progress",... StopTrainingCriteria="EpisodeReward",... StopTrainingValue=-1,... SaveAgentCriteria="EpisodeReward",... SaveAgentValue=-2.5);
Fix the random stream for reproducibility.
rng(0,"twister");Train the agent using the train function. Training is a computationally intensive process that takes several hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining = false; if doTraining % Train the agent. trainingStats = train(agent,env,trainingOpts); else % Load the pretrained agent for the example. load("SimulinkLKADQNMulti.mat","agent"); end
Simulate DQN Agent
Fix the random stream for reproducibility.
rng(0,"twister");To validate the performance of the trained agent, uncomment the following two lines and simulate the agent within the environment. For more information on agent simulation, see rlSimulationOptions and sim.
% simOptions = rlSimulationOptions(MaxSteps=maxsteps); % experience = sim(env,agent,simOptions);
To demonstrate the trained agent on deterministic initial conditions, simulate the model in Simulink.
e1_initial = -0.4; e2_initial = 0.2; sim(mdl)
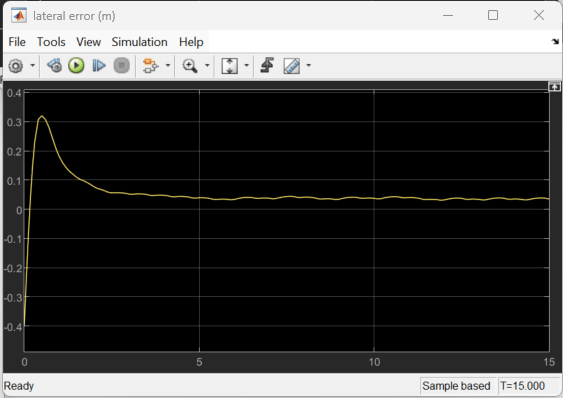
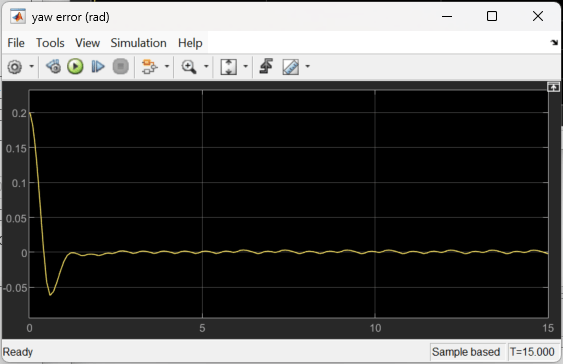
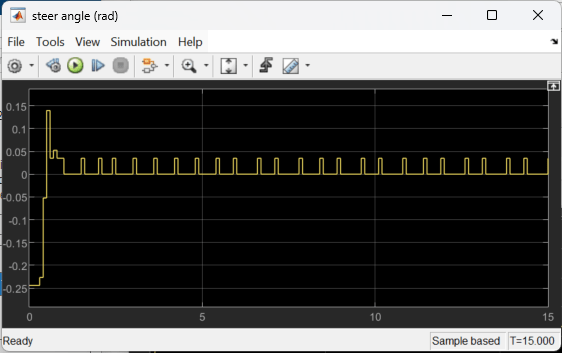
As the plots show, the lateral error (top plot) and relative yaw angle (bottom plot) are both driven close to zero. The vehicle starts from off the centerline (–0.4 m) and with a nonzero yaw angle error (0.2 rad). The lane keeping assist makes the ego car travel along the centerline after about 2.5 seconds. The steering angle (middle plot) shows that the controller reaches steady state after about 2 seconds.
Restore the random number stream using the information stored in previousRngState.
rng(previousRngState);
Reset Function
function in = localResetFcn(in) % reset lateral deviation and relative yaw angle to random values in = setVariable(in,"e1_initial", 0.5*(-1+2*rand)); in = setVariable(in,"e2_initial", 0.1*(-1+2*rand)); end
See Also
Functions
train|sim|rlSimulinkEnv
Objects
Blocks
Topics
- Train DQN Agent for Lane Keeping Assist Using Parallel Computing
- Train PPO Agent with Curriculum Learning for a Lane Keeping Application
- Train DDPG Agent for Path-Following Control
- Lane Keeping Assist System Using Model Predictive Control (Model Predictive Control Toolbox)
- Create Policies and Value Functions
- Deep Q-Network (DQN) Agent
- Train Reinforcement Learning Agents