Manipulator Shape Tracing in MATLAB and Simulink
This example shows how to trace a predefined 3-D shape in space. Following a smooth, distinct path is useful in many robotics applications such as welding, manufacturing, or inspection. A 3-D trajectory is solved in the task space for tracing the MATLAB® membrane and is executed using the Sawyer robot from Rethink Robotics®. The goal is to generate a smooth path for the end effector of the robot to follow based on a set of waypoints.
The Trajectory Control Modeling with Inverse Kinematics example shows how to generate a closely discretized set of segments that can then be passed to an inverse kinematics solver to be solved using an iterative solution. However, this example offers an alternate approach to reduce computational complexity. This example splits path segments into just a few discrete points and uses smoothing functions to interpolate between the waypoints. This approach should generate a smoother trajectory and improve run-time efficiency.
Load the Robot
This example uses the Sawyer robot from Rethink Robotics®. Import the URDF file that specifies the rigid body dynamics. Set the DataFormat to use column vectors to define robot configurations. Simulink® uses column vectors. The task space limits are defined based on empirical data.
sawyer = loadrobot("rethinkSawyer",DataFormat="column"); taskSpaceLimits = [0.5 0.75; -0.125 0.125; 0.25 0.5]; numJoints = 8; % Number of joints in robot
Generate Set of Task-Space Waypoints
For this example, the goal is to get a set of path segments that trace the MATLAB® membrane logo. The membrane surface and the path segments are generated as cell arrays using the helper function generateMembranePaths. To visualize the paths overlaid on the surface, plot the surface using surf and the path segments by iterating through the path segment cell array. You can increase numSamples to sample more finely across the surface.
numSamples = 7; [pathSegments,surface] = generateMembranePaths(numSamples,taskSpaceLimits); % Visualize the output figure surf(surface{:},FaceAlpha=0.3,EdgeColor="none"); title("Path Segments Plotted on L-Membrane") hold on for i=1:numel(pathSegments) segment = pathSegments{i}; plot3(segment(:,1),segment(:,2),segment(:,3),"x-",LineWidth=2); end hold off
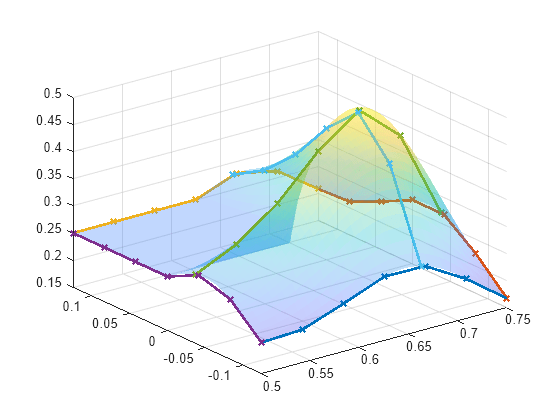
To ensure that the robot can trace the output, visualize the shape in the robot workspace. Show the sawyer robot and plot the line segments in the same figure.
figure show(sawyer); hold on title("Path Segments Plotted in Robot Workspace") for i=1:numel(pathSegments) segment = pathSegments{i}; plot3(segment(:,1),segment(:,2),segment(:,3),"x-",LineWidth=2); end view(135,20) axis([-0.25 1 -.5 .5 -0.1 .75]) hold off

Create an Inverse Kinematics Solver
Create an inverse kinematics (IK) using the loaded sawyer rigid body tree. It is initially configured with a uniform set of weights, using the home configuration as the initial guess. Set the initial guess to the home configuration and the pose tolerances with uniform weights. The end effector for IK solver is the "right_hand" body of the robot.
s=rng(0); % Capture the current seed and seed the rng to 0. ik = inverseKinematics(RigidBodyTree=sawyer); ik.SolverParameters.AllowRandomRestarts = false; initialGuess = sawyer.homeConfiguration; weights = [1 1 1 1 1 1]; eeName = "right_hand";
Convert Task-Space Waypoints to Joint-Space Using Inverse Kinematics
Use the inverse kinematics solver to generate a set of joint space waypoints, which give the joint configurations for the robot at each point of the generated pathSegments. Each joint-space segment is filed into a matrix, jointPathSegmentMatrix, which is passed to the Simulink model as an input.
% Initialize the output matrix jointPathSegmentMatrix = zeros(length(pathSegments),numJoints,numSamples); % Define the orientation so that the end effector is oriented down sawyerOrientation = axang2rotm([0 1 0 pi]); % Compute IK at each waypoint along each segment for i = 1:length(pathSegments) currentTaskSpaceSegment = pathSegments{i}; currentJointSegment = zeros(numJoints, length(currentTaskSpaceSegment)); for j = 1:length(currentTaskSpaceSegment) pose = [sawyerOrientation currentTaskSpaceSegment(j,:)'; 0 0 0 1]; currentJointSegment(:,j) = ik(eeName,pose,weights,initialGuess); initialGuess = currentJointSegment(:,j); end jointPathSegmentMatrix(i,:,:) = (currentJointSegment); end
Load Simulink Model
Use the shapeTracingSawyer model to execute the trajectories and simulate them on a kinematic model of the robot.
open_system("shapeTracingSawyer.slx")The Simulink model has two main parts:
The Trajectory Generation section takes the matrix of joint-space path segments, jointPathSegmentMatrix, and converts the segments to a set of discretized joint-space waypoints (joint configurations) at each time step in the simulation using a MATLAB function block. The Polynomial Trajectory Block converts the set of joint configurations to a smoothed joint space B-spline trajectory in time.
The Robot Kinematics Simulation section accepts the joint-space waypoints from the smoothed trajectory and computes the resulting end-effector position for the robot.
Trajectory Generation

Robot Kinematics Simulation

Execute Joint-Space Trajectories in Simulink
Simulate the model to execute the generate trajectories.
sim("shapeTracingSawyer.slx")View Trajectory Generation Results
The model outputs the robot joint configurations and the end-effector positions along each smoothed path trajectory. To work easily with MATLAB plotting tools, reshape the data.
% End effector positions xPositionsEE = reshape(eePosData.Data(1,:,:),1,size(eePosData.Data,3)); yPositionsEE = reshape(eePosData.Data(2,:,:),1,size(eePosData.Data,3)); zPositionsEE = reshape(eePosData.Data(3,:,:),1,size(eePosData.Data,3)); % Extract joint-space results jointConfigurationData = reshape(jointPosData.Data,numJoints,size(eePosData.Data,3));
Plot the new end-effector positions on the original membrane surface.
figure
surf(surface{:},FaceAlpha=0.3,EdgeColor="none");
hold on
plot3(xPositionsEE,yPositionsEE,zPositionsEE)
grid on
title(["Smoothed End-Effector Trajectories","Plotted on L-Membrane Surface"])
hold off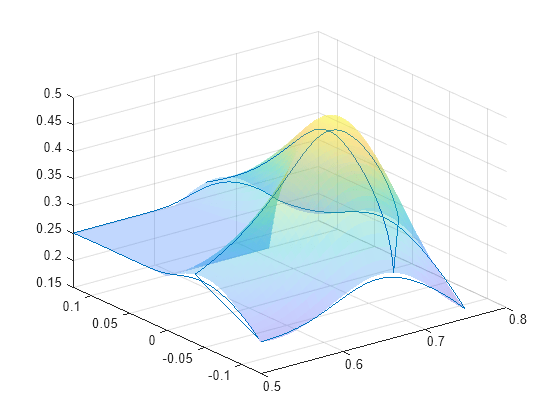
Visualize Robot Motion
In addition to the visualization above, the tracing behavior can be recreated using the Sawyer robot model. Iterate through the joint configurations in jointConfigurationData to visualize the robot using show and continuously plot the end-effector position in 3-D space.
% For faster visualization, only display every few steps vizStep = 5; % Initialize a new figure window figure set(gcf,Visible="on"); title("Sawyer Tracing L-Membrane") % Iterate through all joint configurations and end-effectort positions for i = 1:vizStep:length(xPositionsEE) show(sawyer, jointConfigurationData(:,i),Frames="off",PreservePlot=false); hold on plot3(xPositionsEE(1:i),yPositionsEE(1:i),zPositionsEE(1:i),"b",LineWidth=3) view(135,20) axis([-1 1 -.5 .5 -1 .75]) drawnow end hold off
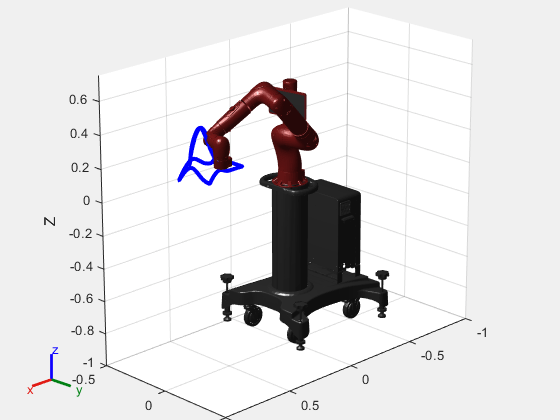
rng(s); % restore the global state of the random number generator