Using Numerical Compensation for Co-Simulation Integration

This example shows how to reduce potential simulation errors introduced by co-simulation using numerical compensation.

An Example Co-Simulation Component

A typical co-simulation component can be represented by a dynamic system with continuous states and a local solver that performs integration between communication time points. These functions export the standalone Co-Simulation FMU cosim_component.fmu from this model:

componentMdl = 'cosim_component';
open_system(componentMdl);

This model contains a transfer function and has a local fixed-step solver with step size ts=0.02s. You can use the generated FMU as a co-simulation component in an integration model.

Note that co-simulation components can only use input values given at communication time points. This requirement introduces a co-simulation error when the communication step is relatively large compared to the dynamic behavior of the component. Reducing the communication step size improves the simulation result but increases data transfer overhead. Changing local solver types or reducing local solver step size can give better integration results within a communication step, but cannot compensate for co-simulation error due to undersampling.

Using Numerical Compensation in Integration Model

The co-simulation component is used in the following model for integration:

integrationMdl = 'cosim_integration';
open_system(integrationMdl);
set_param(integrationMdl, 'SimulationCommand', 'Update');

This model contains two connected FMU co-simulation components in the top branch. Both co-simulation components, FMU Cosim Component 1 and FMU Cosim Component 2, have their own local solver. They only exchange data at a discretized communication rate D2, where ts=0.2s. Two continuous-time Transfer Function blocks in the bottom branch are the monolithic, non-co-simulation approach of the same system, which uses the global solver and serves as the baseline for the simulation result. The two non-co-simulation components exchange data at a continuous rate, and the global solver step size is set to ts=0.02s. In this example, we focus on the numerical behavior of FMU Cosim Component 2 and assume that co-simulation discretization of its input signal is inevitable.

After updating block diagram, a gear icon appears at the input port for the second co-sim component, FMU Cosim Component 2. This indicates that Simulink has automatically determined that this input port needs numerical compensation because:

• Source (and destination) blocks declare their output (and non-directfeedthrough input) ports as continuous quantities.

• Source and destination blocks are co-simulation components (e.g. S-Function or Co-Simulation FMU)

• The signal has a double data type and periodic discrete sample rate

To turn off auto-compensation,left-click on the icon. Alternatively, to programmatically turn it off:

blk = 'cosim_integration/FMU Cosim Component 2';
p = get_param(blk, 'PortHandles')

p = struct with fields:
      Inport: 321.0026
     Outport: 320.0027
      Enable: []
     Trigger: []
       State: []
       LConn: []
       RConn: []
    Ifaction: []
       Reset: []
       Event: []

set_param(p.Inport,'CoSimSignalCompensationMode','Auto_Off')
out_off = sim(integrationMdl);

Simulink does not compensate for co-simulation error on this input port when the gear icon appears as disabled. The following functions plot the result without numerical compensation:

figure(1); hold on;
plot(out_off.yout{1}.Values,'r');
plot(out_off.yout{2}.Values,'black');
plot(out_off.yout{3}.Values,'g');
plot(out_off.yout{4}.Values,'b');
legend({'cosim response(no compensation)', 'ideal response', 'cosim input', 'ideal input'}, 'Location', 'northwest')

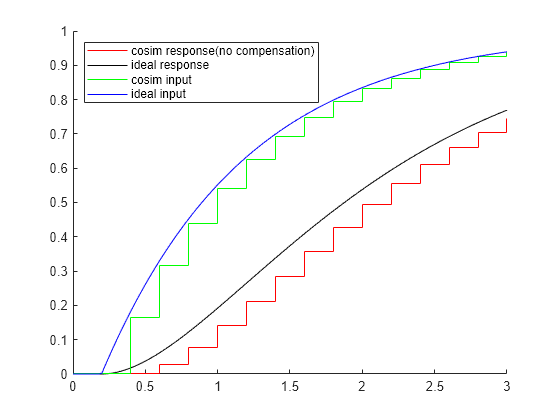
The co-simulation input signal (a double-typed periodic discrete signal that represents a continuous quantity) jumps from 0 to a positive value at t=0.4s. The co-simulation response shows a delay to its input when compared to the ideal (non-co-simulation) response. The co-simulation scheme causes this delay, where the input signal cannot vary between two communication time points. For example, when co-simulation component FMU Cosim Component 2 pauses at communication time point t=0.4s, the local solver takes a positive input for integration; then the local solver integrates over communication step [0.4,0.6], and returns a positive output value at the next communication time point t=0.6s.

When numerical compensation is enabled, Simulink attempts to compute a better input value for co-simulation component FMU Cosim Component 2 so that the co-simulation input value is closer to the average non-co-simulation input between two communication time points. For example, instead of using the co-simulation input value y=0.165 at t=0.4s, a better averaged input over communication step [0.4,0.6] is somewhere around y=0.241, which is the midpoint of y=0.165(t=0.4s) and y=0.316(t=0.6s). This is like using the midpoint Riemann sum instead of the left sum to estimate the area under the curve of an ideal input signal.

However, at communication time point t=0.4s, the value of y=0.316(t=0.6s) is still not available. To get an estimate of y value at t=0.6s, Simulink extrapolates the signal data as a polynomial based on earlier time points (e.g. t=0.2s, t=0.4s). You can select a different extrapolation method in Co-simulation Numerical Compensation dialog when right-clicking the icon. Alternatively, use the functions:

set_param(p.Inport,'CoSimSignalCompensationConfig','{"ExtrapolationMethod":"LinearExtrapolation"}')

The following plot compares the result of enabling or disabling the compensation:

set_param(p.Inport,'CoSimSignalCompensationMode','Auto')
out_linear = sim(integrationMdl);
figure(2); hold on;
plot(out_off.yout{1}.Values,'r')
plot(out_linear.yout{1}.Values, 'm')
plot(out_off.yout{2}.Values,'black')
legend({'cosim response(no compensation)', 'cosim response(linear extrapolation)', 'ideal response'}, 'Location', 'northwest')

With numerical compensation, the co-simulation response at communication timepoints are much closer to the ideal non-co-simulation output. The numerical error (delay) introduced by co-simulation is reduced.

The following plot shows the impact of the different extrapolation methods:

set_param(p.Inport,'CoSimSignalCompensationConfig','{"ExtrapolationMethod":"QuadraticExtrapolation"}')
out_quadratic = sim(integrationMdl);
set_param(p.Inport,'CoSimSignalCompensationConfig','{"ExtrapolationMethod":"CubicExtrapolation"}')
out_cubic = sim(integrationMdl);
figure(3); hold on;
plot(out_linear.yout{1}.Values,'r')
plot(out_quadratic.yout{1}.Values, 'g')
plot(out_cubic.yout{1}.Values, 'b')
plot(out_off.yout{2}.Values,'black')
legend({'cosim response(linear extrapolation)','cosim response(quadratic extrapolation)','cosim response(cubic extrapolation)','ideal response'},'Location','northwest')

The extrapolated output value introduces an estimation error, for example, when comparing extrapolated y value at t=0.6s (estimated at t=0.4s) to the real y value at t=0.6s (recorded at t=0.6s). Simulink can optionally compensate for this error in the following communication steps when you specify a non-zero signal correction coefficient in Co-simulation Numerical Compensation dialog. Alternatively, use these functions:

set_param(p.Inport,'CoSimSignalCompensationConfig','{"ExtrapolationMethod":"LinearExtrapolation", "CompensationCoefficient":"1"}')

This coefficient is valid within [0,1], where 0 means the estimation error will be ignored, and 1 means estimation error is fully compensated in the following communication steps. Setting this value to 1 might be useful when the co-simulation signal represents, or is proportional to, a flux of some conserved quantity (e.g. current, mass or volumetric flow rate).

The following plot shows the impact of different values of the signal correction coefficient:

set_param(p.Inport,'CoSimSignalCompensationConfig', '{"ExtrapolationMethod":"LinearExtrapolation", "CompensationCoefficient":"0"}' )
out_linear_0 = sim(integrationMdl);
set_param(p.Inport,'CoSimSignalCompensationConfig', '{"ExtrapolationMethod":"LinearExtrapolation", "CompensationCoefficient":"0.5"}' )
out_linear_0_5 = sim(integrationMdl);
set_param(p.Inport,'CoSimSignalCompensationConfig', '{"ExtrapolationMethod":"LinearExtrapolation", "CompensationCoefficient":"1"}' )
out_linear_1 = sim(integrationMdl);
figure(4); hold on;
plot(out_linear_0.yout{1}.Values,'r')
plot(out_linear_0_5.yout{1}.Values, 'g')
plot(out_linear_1.yout{1}.Values, 'b')
plot(out_off.yout{2}.Values,'black')
legend({'cosim response(coefficient: 0)','cosim response(coefficient: 0.5)','cosim response(coefficient: 1)','ideal response'},'Location','northwest')

close_system(componentMdl, 0);
close_system(integrationMdl, 0);