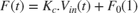Variable Pulse Generator
Generate ideal, time varying pulse signal
Libraries:
Simulink /
Discontinuities
Description
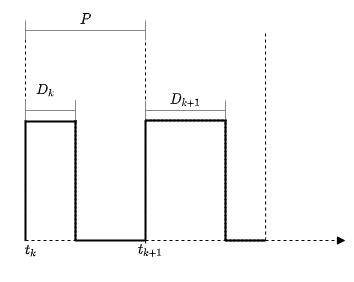
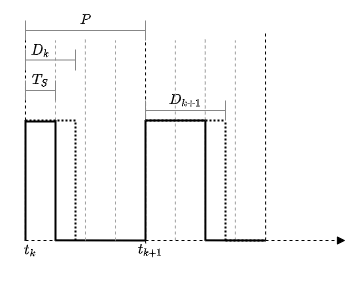
Use the Variable Pulse Generator block to create ideal modulated pulse signals.
Generally speaking, the output pulse of the block is described by
where pw is the output pulse width.
For an implementation of Pulse Width Modulation, see PWM.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Algorithms
Extended Capabilities
Version History
Introduced in R2020b