Vectorizing a Scalar Algorithm with a For-Each Subsystem

This example shows how to use the for-each subsystem. In this example, the operations are performed on a vector for simplicity.

Open the example model named sldemo_foreach_vectorized. This model contains a for-each subsystem that processes the input signals one by one.

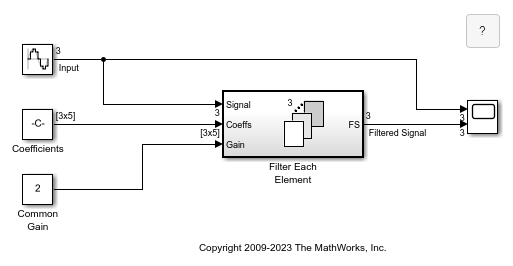
The inputs to the for-each subsystem are the signals to process, the coefficients of the FIR filter to use with each of these signals, and the common gain.

Each signal is scalar and needs to be processed individually. Consequently, the For Each block that controls the partition dimension is set to partition the input signal along dimension 1 by slicing through a partition width of 1. For each input signal, a corresponding set of coefficients must also be partitioned using the same criteria. The gain is common to all the signals, so this input is not partitioned.

Since the output signal dimension is expected to match the input signal dimension, the concatenation dimension is set equal to the partition dimension. If you prefer to change the signal dimension, a transpose in this case, you can choose 2 as the concatenation dimension.

For the for-each subsystem, you must set the partition dimension and width, but not the input signal size. A check then ensures that this size is a multiple of the partition width. If no error is detected, the subsystem then calculates the number of independent executions that the enclosed subsystem will perform. These executions are independent in that the state associated with a given block contained in the subsystem has a unique value in each of the respective executions.

To see a non-vectorized implementation for this model, open the example model named sldemo_foreach_repeat_scalar.

This implementation does not use the for-each subsystem but mimics its functionality in these ways:

• By replicating the subsystem as many times as necessary

• By selecting and concatenating the signals appropriately

This replication process is prone to error and is not scalable. Changing the input signal size would require changing the model accordingly.