Design Active Disturbance Rejection Control for BLDC Speed Control Using PWM
This example shows how to design active disturbance rejection control (ADRC) of the speed of a brushless DC (BLDC) motor modeled in Simulink® using Simscape™ Electrical™ components.
In this example, you also compare the control performance of the ADRC controller with a PID controller. Although you can tune the PID controller over a wide operating range, designing experiments and tuning PID gains require significant efforts. Using ADRC you can obtain a nonlinear controller and achieve better performance with a simpler setup and less tuning effort.
BLDC Motor Model
BLDC motors offer many advantages over their brushed counterparts, such as higher efficiency and lower maintenance. The speed of this BLDC motor is controlled by implementing PWM control. To control the motor speed, an ideal DC voltage source is modulated using pulse width modulation (PWM) and sent through a three-phase inverter to drive the BLDC motor. This model is based on the model discussed in the BLDC Speed Control Using PWM video.
mdl = 'BLDCMotorADRC';
open_system(mdl)
This model contains a controller variant subsystem with two choices: an ADRC controller and a PID controller. The ADRC Controller subsystem is set as the default active variant. The model also includes a manual switch to operate the model in open-loop and closed-loop configurations. It is set to an open-loop configuration by default.

In this model, a PWM control is implemented by modulating the phase voltages directly. A PWM Generator block is used under the Commutation Logic subsystem. According to this logic, the PWM Generator block's output helps the DC source voltage of 500 V pulse on and off to energize the correct phases based on the sector the rotor is in.
Design ADRC Controller
ADRC is a powerful tool for the controller design of a plant with unknown dynamics and internal and external disturbances. The block models unknown dynamics and disturbances as an extended state of the plant and estimates them using an observer. The block lets you design a controller using only a few key tuning parameters for the control algorithm:
Model order type (first-order or second order)
Critical gain of the model response
Controller and observer bandwidths
Additionally, you specify the Time domain parameter to match the time domain of the plant model. In this example, it is set to discrete-time with a sample time equal to the Ts_motor variable provided with the model. The following sections describe how to find the remaining tuning parameters specified in the ADRC block parameters for this model.

Model Order and Critical Gain
To identify the model order, simulate the plant model in the open-loop configuration. Assume the saturation limits of the duty cycle from 0 to 1 and use a step input of 0.5 as duty cycle to drive the plant model.
set_param(mdl,'SignalLoggingName','openLoopSim'); sim(mdl); stepRef = getElement(openLoopSim,'stepRef'); speedOut = getElement(openLoopSim,'Measured speed'); figure; plot(stepRef.Values.Time,stepRef.Values.Data... ,speedOut.Values.Time,speedOut.Values.Data) grid on xlabel('Time (s)') ylabel('Speed (RPM)') legend('Ref','Output')
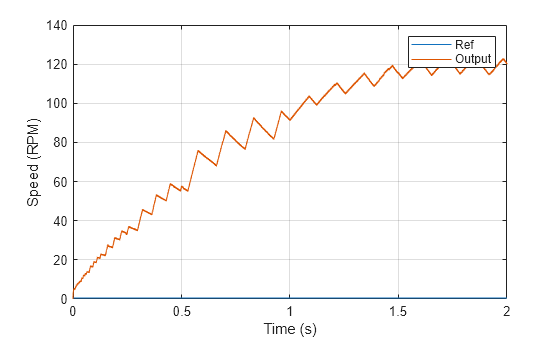
To determine the critical gain value b0, examine the speed response over a short interval of 0.00075 seconds right after the step reference input.
x = speedOut.Values.Time(1:16); y = speedOut.Values.Data(1:16); figure plot(x,y) xlabel('Time (s)') ylabel('Speed(RPM)') grid on
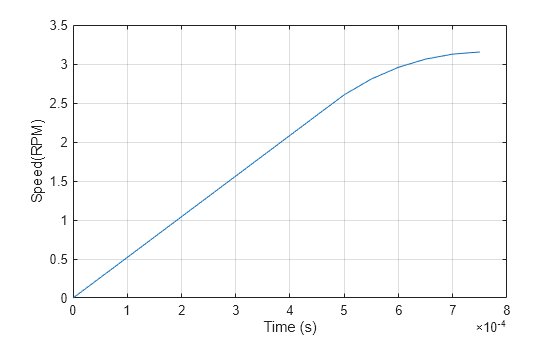
y(end)
ans = 2.8890
The speed response shows a typical shape for a second-order dynamic system. As a result, select second-order for the Model type parameter. Based on the measured speed, you can determine the critical gain through the second-order response approximation . Over a duration of 0.0005 seconds, the speed changes by 3.1542 rpm.
a = 2*y(end)/(x(end)^2); b0 = a/0.5;
Controller Bandwidth and Observer Bandwidth
The controller bandwidth usually depends on the performance specifications, either in the frequency domain or time domain. In this example, the controller bandwidth is set to 1000 rad/s.
In general, the observer bandwidth is set to 5 to 10 times so that the observer converges faster than the controller. In this example, specify the observer bandwidth to be the same as the controller bandwidth. Doing so allows you to take advantage of the observer to filter out the excessive switching noise present in a BLDC motor controlled with PWM. The following figure shows the ADRC controller output duty cycle signal when the observer bandwidth is set to 1000 rad/s and 5000 rad/s.
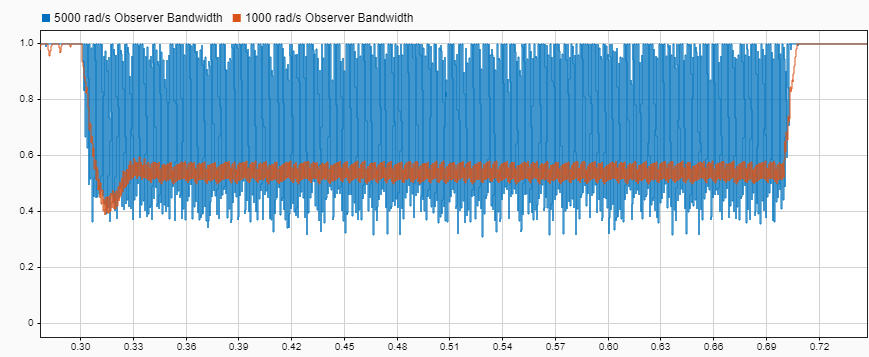
You can see that the ADRC block's output signal has much less noise when observer bandwidth is 1000 rad/s as compared to 5000 rad/s. Having such a noisy duty cycle output can render the controller unusable in realistic systems.
Although reducing the observer bandwidth reduces the oscillation in ADRC block's output signal, further reducing may not be possible because the overall control performance can be adversely impacted by the slow convergence of the observer.
Performance Comparison of ADRC and PID Controller
You can examine the tuned controller performance using a simulation with changing speed reference signals.
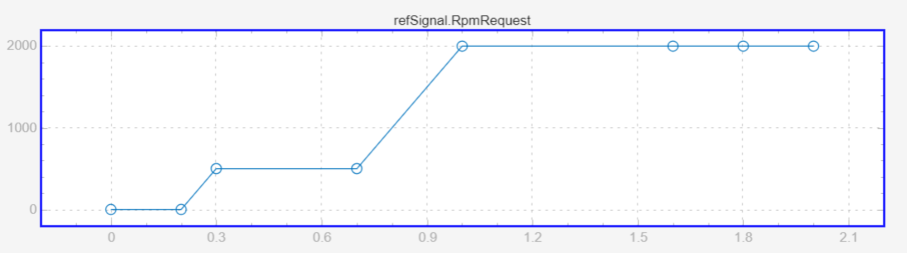
To examine the dynamic performance of controllers, the model undergoes the following acceleration processes.
Between t = 0.2 s and t = 0.3 s, the speed reference ramps from 0 rpm to 500 rpm.
Between t = 0.7 s and t = 1.0 s, the speed reference ramps from 500 rpm to 2000 rpm.
Toggle the manual switch to operate the model in the closed-loop configuration.
set_param('BLDCMotorADRC/Manual Switch','sw','0')
Simulate the model with the ADRC Controller subsystem.
set_param(mdl,'SignalLoggingName','adrcSim'); sim(mdl); speedOutADRC = getElement(adrcSim,'Measured speed');
Simulate the model with the PID Controller subsystem.
set_param([mdl,'/Controller'],'LabelModeActiveChoice','PID') set_param(mdl,'SignalLoggingName','pidSim'); sim(mdl); speedOutPID = getElement(pidSim,'Measured speed');
Compare the performance of the two controllers.
figure;
plot(refSignal{1}.Time,refSignal{1}.Data...
,speedOutADRC.Values.Time,speedOutADRC.Values.Data)
hold on
plot(speedOutPID.Values.Time,speedOutPID.Values.Data)
hold off
grid on
xlabel('Time (s)')
ylabel('Speed (RPM)')
legend('Ref','ADRC','PID','location','best')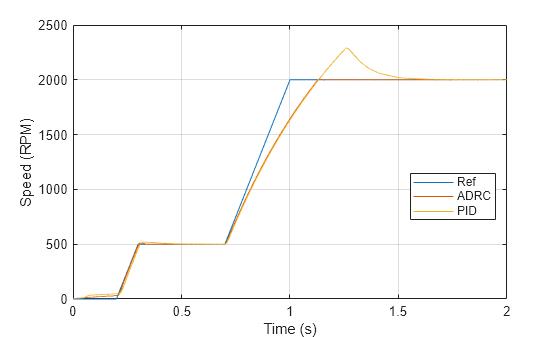
The speed response shows that the ADRC controller performs much better than the PID controller by following the speed reference more closely during transients and reducing the overshoot around 2000 rpm.
Close the model.
close_system(mdl,0);
See Also
Active Disturbance Rejection Control