Probability Distribution Function Tool
Interactive density and distribution plots
Description
The Probability Distribution Function tool creates an interactive plot of the cumulative distribution function (cdf) or probability density function (pdf) for a probability distribution. Explore the effects of changing parameter values on the shape of the plot, either by specifying parameter values or using interactive sliders.
Required Products
MATLAB®
Statistics and Machine Learning Toolbox™
Note:
disttool does not provide printing, code generating, or data
importing functionality in MATLAB
Online™.
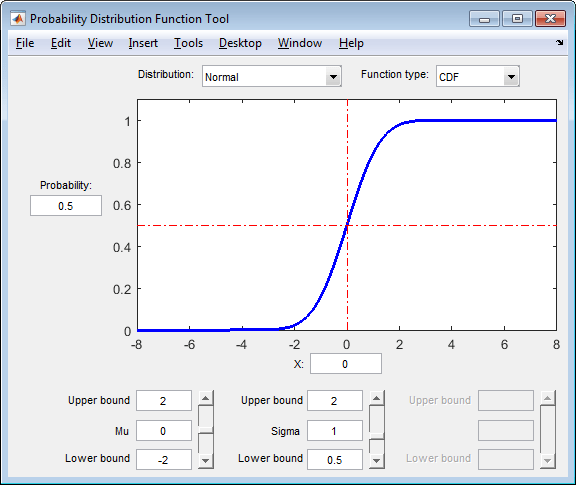
Open the Probability Distribution Function Tool
At the command prompt, enter
disttool.
Examples
This example shows how to use the Probability Distribution Function Tool to explore the shape of cdf and pdf plots for different probability distributions and parameter values.
Open the Probability Distribution Function tool.
disttool

The interface opens with a plot of the cdf of the Normal distribution. The
initial parameter settings are Mu = 0 and Sigma
= 1.
Select PDF from the Function
type drop-down menu to plot the pdf of the Normal
distribution using the same parameter values.

Change the value of the location parameter Mu to
1.
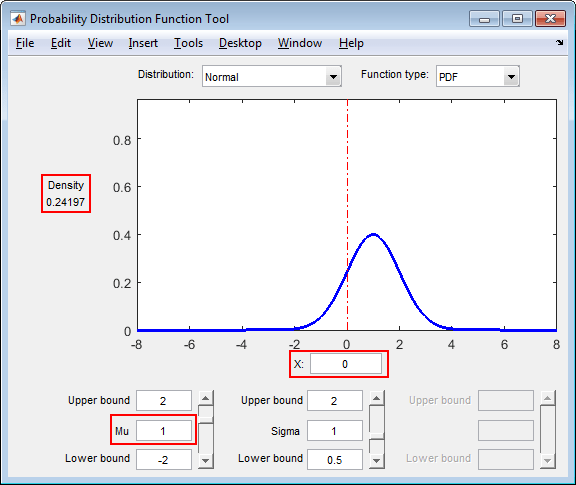
As the parameter values change, the shape of the plot also changes. Also,
the value of X remains the same, but the density value
changes because of the new parameter value.
Use the Distribution drop-down menu to change the
distribution type from Normal to
Weibull.
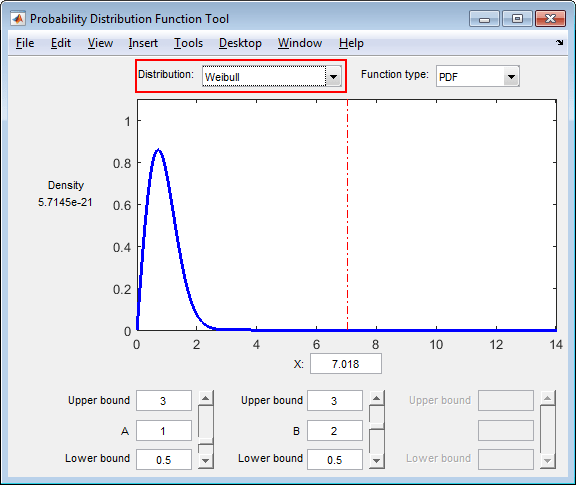
The shape of the plot changes, along with the names and values of the parameters.
Parameters
Specify the probability distribution to explore by selecting a
distribution name from the drop-down list. The drop-down list includes
approximately 25 probability distribution options, including
Normal,
Exponential,
Poisson, Weibull,
and more.
Specify the probability distribution function type as
CDF (cumulative distribution function) or
PDF (probability density function) by
selecting the function name from the drop-down list.
Specify the cumulative distribution function (cdf) value of interest as a numeric value in the range [0,1]. The corresponding random variable value appears in the X field below the plot. Alternatively, you can specify a value for X, and the Probability value will update automatically.
This option only appears if Function type is
CDF. If Function type is
PDF, then the probability density at the
specified X value displays to the left of the
plot.
Specify the random variable of interest as a numeric value. If the
Function type is CDF,
then the corresponding cumulative distribution function (cdf) value appears
in the Probability field to the left of the plot.
Alternatively, you can specify a value for Probability,
and the X value will update automatically. If the
Function type is PDF,
then the corresponding probability density value appears to the left of the
plot.
Specify the parameter boundaries and values as numeric values. Each column
contains a field for the upper bound, value, and lower bound of one
parameter. The name and number of available parameters changes based on the
distribution specified in the Distribution drop-down
list. For example, if you select the Normal
distribution, then disttool enables two columns: One
column for the Mu parameter and one column for the
Sigma parameter. If you select the
Exponential distribution, then
disttool enables one column for the
Mu parameter.
Tips
To change the value of X (on the y-axis), or Probability or Density (on the x-axis):
Type the values of interest into the Probability or X fields;
Click on the point of interest on the plot; or
Click and drag the reference lines across the plot.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)