mod
Symbolic modulus after division
Starting in R2020b, mod no longer finds the modulus for each
coefficient of a symbolic polynomial. For more information, see Version History.
Syntax
Description
Examples
Find the modulus after division when both the dividend and divisor are integers.
Find the modulus after division for these numbers.
m = [mod(sym(27),4), mod(sym(27),-4), mod(sym(-27),4), mod(sym(-27),-4)]
m =
Find the modulus after division when the dividend is a rational number, and the divisor is an integer.
Find the modulus after division for these numbers.
m = [mod(sym(22/3),5), mod(sym(1/2),7), mod(sym(27/6),-11)]
m =
Find the modulus after division when the dividend is a polynomial expression, and the divisor is an integer. If the dividend is a polynomial expression, then mod returns a symbolic expression without evaluating the modulus.
Find the modulus after division by for the polynomial .
syms x
a = x^3 - 2*x + 999;
mUneval = mod(a,10)mUneval =
To evaluate the modulus for each polynomial coefficient, first extract the coefficients of each term using coeffs.
[c,t] = coeffs(a)
c =
t =
Next, find the modulus of each coefficient in c divided by 10. Reconstruct a new polynomial using the evaluated coefficients.
cMod10 = mod(c,10); mEval = sum(cMod10.*t)
mEval =
For vectors and matrices, mod finds the modulus after division element-wise. When both arguments are nonscalar, they must have the same size. If one argument is a scalar, the mod function expands the scalar input into an array of the same size as the other input.
Find the modulus after division for the elements of two matrices.
A = sym([27,28; 29,30]); B = sym([2,3; 4,5]); M = mod(A,B)
M =
Find the modulus after division for the elements of matrix A and the value 9. Here, mod expands 9 into the 2-by-2 matrix with all elements equal to 9.
M = mod(A,9)
M =
Create two periodic functions that represents sawtooth waves.
Define the sawtooth wave with period T = 2 and amplitude A = 1.5. Create a symbolic function y(x). Use mod functions to define the sawtooth wave for each period. The sawtooth wave increases linearly for a full period, and it drops back to zero at the start of another period.
T = 2;
A = 1.5;
syms y(x);
y(x) = A*mod(x,T)/T;Plot this sawtooth wave for the interval [-6 6].
fplot(y,[-6 6])

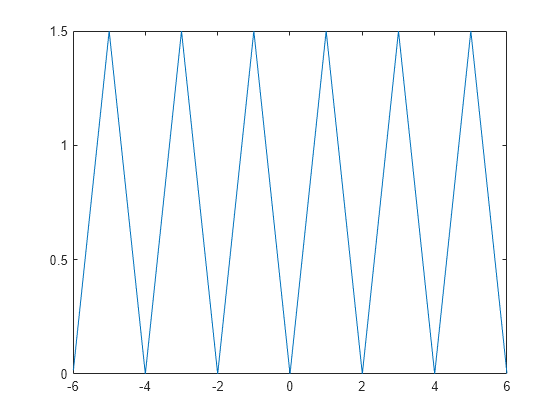
Next, create another sawtooth wave that is symmetrical within a single period. Use piecewise to define the sawtooth wave that is increasing linearly for the first half of a period, and then decreasing linearly for the second half of a period.
y(x) = piecewise(0 < mod(x,T) <= (T/2), 2*A*mod(x,T)/T,...
(T/2) < mod(x,T) <= T, 2*A - 2*A*mod(x,T)/T);Plot this sawtooth wave for the interval [-6 6].
fplot(y,[-6 6])
Input Arguments
Dividend (numerator), specified as a number, symbolic number, variable,
polynomial expression, or a vector or matrix of numbers, symbolic numbers,
variables, or polynomial expressions. Inputs a and
b must be the same size unless one is a scalar. The
function expands a scalar input into an array of the same size as the other
input.
Divisor (denominator), specified as a number, symbolic number, or a vector
or matrix of numbers or symbolic numbers. Inputs a and
b must be the same size unless one is a scalar. The
function expands a scalar input into an array of the same size as the other
input.
More About
The modulus of a and b is
where floor rounds (a / b) toward negative infinity. For example, the modulus of –8 and –3 is
–2, but the modulus of –8 and 3 is 1.
If b = 0, then mod(a, b) = mod(a, 0) = 0.
Tips
Calling
modfor numbers that are not symbolic objects invokes the MATLAB®modfunction.
Version History
Introduced before R2006aStarting in R2020b, mod no longer finds the modulus for each
coefficient of a symbolic polynomial. Instead, mod(a,b) returns
an unevaluated symbolic expression if a is a symbolic polynomial
and b is a real number. To find the modulus for each coefficient
of the polynomial a, use [c,t] = coeffs(a);
sum(mod(c,b).*t). You can now create periodic symbolic functions by
defining the periodicity using mod. For example, see Create Periodic Sawtooth Waves.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)