1-D Multisignal Analysis
This section takes you through the features of 1-D multisignal wavelet analysis, compression and denoising using the Wavelet Toolbox™ software. The rationale for each topic is the same as in the 1-D single signal case.
The toolbox provides the following functions for multisignal analysis.
Analysis-Decomposition and Synthesis-Reconstruction Functions
Decomposition Structure Utilities
Function Name | Purpose |
|---|---|
Change multisignal 1-D decomposition coefficients | |
Multisignal 1-D decomposition energy repartition |
Compression and Denoising Functions
1-D Multisignal Analysis
Load an image file, and display its dimensions. For purposes of this example, unless stated otherwise, you will treat the data as a multisignal. Each row of the image is one signal.
load thinker
size(X)ans = 1×2
192 96
Plot some signals from the data.
plot(X(1:5,:)',"r") hold on plot(X(21:25,:)',"b") plot(X(31:35,:)',"g") hold off xlim([1 96]) grid on

Decomposition and Reconstruction
Use mdwtdec to perform a wavelet decomposition of the multisignal at level 2 using the db2 wavelet.
dec = mdwtdec("r",X,2,"db2")
dec = struct with fields:
dirDec: 'r'
level: 2
wname: 'db2'
dwtFilters: [1×1 struct]
dwtEXTM: 'sym'
dwtShift: 0
dataSize: [192 96]
ca: [192×26 double]
cd: {[192×49 double] [192×26 double]}
Use chgwdeccfs to generate a new wavelet decomposition structure from dec. For each signal, change the wavelet coefficients by setting all the coefficients of the detail of level 1 to zero.
decBIS = chgwdeccfs(dec,"cd",0,1);Use mdwtrec to perform a wavelet reconstruction of the multisignal. Plot some of the new signals.
Xbis = mdwtrec(decBIS); plot(Xbis(1:5,:)',"r") hold on plot(Xbis(21:25,:)',"b") plot(Xbis(31:35,:)',"g") hold off grid on xlim([1 96])

Compare old and new signals by plotting them together.
idxSIG = [1 31]; plot(X(idxSIG,:)',"r",LineWidth=2) hold on plot(Xbis(idxSIG,:)',"b",Linewidth=2) hold off grid on xlim([1 96])

Set the wavelet coefficients at level 1 and 2 for signals 31 to 35 to the value zero, perform a wavelet reconstruction of signal 31, and compare some of the old and new signals.
decTER = chgwdeccfs(dec,'cd',0,1:2,31:35); Y = mdwtrec(decTER,'a',0,31); figure plot(X([1 31],:)',"r",LineWidth=2) hold on plot([Xbis(1,:); Y]',"b",LineWidth=2) hold off grid on xlim([1 96])

Use wdecenergy to compute the energy of signals and the percentage of energy for wavelet components. Display the energy of two of the signals.
[E,PEC,PECFS] = wdecenergy(dec); Ener_1_31 = E([1 31])
Ener_1_31 = 2×1
106 ×
3.7534
2.2411
Compute the percentage of energy for wavelet components of signals 1 and 31. The first column shows the percentage of energy for approximations at level 2. Columns 2 and 3 show the percentage of energy for details at level 2 and 1, respectively.
PEC_1_31 = PEC([1 31],:)
PEC_1_31 = 2×3
99.7760 0.1718 0.0522
99.3850 0.2926 0.3225
Display the percentage of energy for wavelet coefficients of signals 1 and 31. As we can see in the dec structure, there are 26 coefficients for the approximation and the detail at level 2, and 49 coefficients for the detail at level 1.
PECFS_1 = PECFS(1,:); PECFS_31 = PECFS(31,:); plot(PECFS_1,"r",LineWidth=2) hold on plot(PECFS_31,"b",LineWidth=2) hold off grid on xlim([1 size(PECFS,2)])

Compression
Use mswcmp to compress the signals to obtain a percentage of zeros near 95% for the wavelet coefficients.
[XC,decCMP,~] = mswcmp("cmp",dec,"N0_perf",95); [Ecmp,PECcmp,PECFScmp] = wdecenergy(decCMP);
Plot the original signals 1 and 31, and the corresponding compressed signals.
plot(X([1 31],:)',"r",LineWidth=2) hold on plot(XC([1 31],:)',"b",LineWidth=2) hold off grid on xlim([1 96])

Use mswcmptp to compute thresholds, percentage of energy preserved and percentage of zeros associated with the L2_perf method preserving at least 95% of energy.
[THR_VAL,L2_Perf,N0_Perf] = mswcmptp(dec,"L2_perf",95);
idxSIG = [1,31];
Thr = THR_VAL(idxSIG)Thr = 2×1
256.1914
158.6085
L2per = L2_Perf(idxSIG)
L2per = 2×1
96.5488
94.7197
N0per = N0_Perf(idxSIG)
N0per = 2×1
79.2079
86.1386
Compress the signals to obtain a percentage of zeros near 60% for the wavelet coefficients.
[XC,decCMP,~] = mswcmp("cmp",dec,"N0_perf",60);
XC signals are the compressed versions of the original signals in the row direction. Compress the XC signals in the column direction
XX = mswcmp("cmpsig","c",XC,"db2",2,"N0_perf",60);
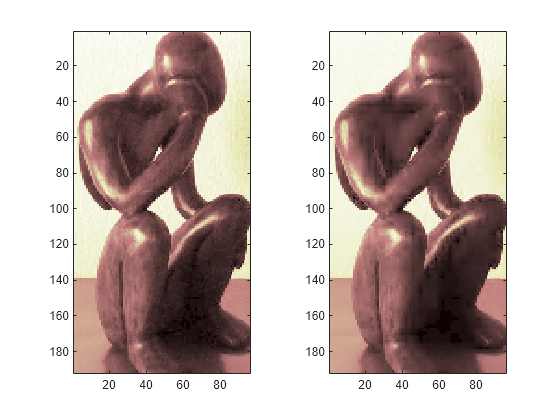
Plot original signals X and the compressed signals XX as images.
tiledlayout(1,2) nexttile image(X) nexttile image(XX) colormap(pink(222))
Denoising
You can use the wdenoise function to denoise a multisignal. By default, wdenoise denoises the columns of matrix. Denoise the multisignal using wdenoise with default settings. Compare with the original signals.
XD = wdenoise(X'); XD = XD'; figure plot(X([1 31],:)',"r",LineWidth=2) hold on plot(XD([1 31],:)',"b",Linewidth=2) hold off grid on xlim([1 96])

References
[1] Denoeud, L., Garreta, H., and A. Guénoche. "Comparison of Distance Indices Between Partitions." In International Symposium on Applied Stochastic Models and Data Analysis, 432–440. Brest, France: École Nationale des Télécommunications de Bretagne, 2005.
See Also
wdenoise | mdwtdec | mdwtrec | mswcmp | mdwtcluster