What Is Quantization?
Quantization is the process of mapping continuous infinite values to a smaller set of discrete finite values. In the context of simulation and embedded computing, it is about approximating real-world values with a digital representation that introduces limits on the precision and range of a value. Quantization introduces various sources of error in your algorithm, such as rounding errors, underflow or overflow, computational noise, and limit cycles. This results in numerical differences between the ideal system behavior and the computed numerical behavior.
To manage the effects of quantization, you need to choose the right data types to represent the real-world signals. You need to consider the precision, range, and scaling of the data type used to encode the signal, and also account for the non-linear cumulative effects of quantization on the numerical behavior of your algorithm. This cumulative effect is further exacerbated when you have constructs such as feedback loops.
Why Quantization Matters
The process of converting a design for embedded hardware needs to take the quantization errors into account. Quantization errors affect signal processing, wireless, control systems, FPGA, ASIC, SoC, deep learning, and other applications.
Quantization in Signal Processing and Wireless Applications
In signal processing applications, quantization errors contribute to noise and degrade the signal to noise ratio (SNR). The SNR is measured in dB and is generally described as x decibel reduction for each additional bit. In order to manage quantization noise and keep it at an acceptable level, you need to choose the right settings such as the data types and rounding modes.
Quantization in Control Systems
When designing control systems, particularly for low-power microcontrollers, you can use integer or fixed-point arithmetic to balance real-time performance requirements with the low-power constraints. In such designs, you need to choose data types that accommodate the dynamic range and precision of the signals coming from input sensors while meeting the precision requirements for the output signals, all without running into numerical differences due to quantization.

Quantized model for a permanent magnet synchronous motor for field-oriented control (see example).
Quantization in FPGA, ASIC, and SoC Development
Converting a design from floating point to fixed point can help minimize power and resource consumption by reducing the FPGA resource utilization, lowering power consumption, meeting latency requirements, etc. However, this conversion introduces quantization errors, and so you must budget the quantization noise appropriately when converting your designs.

Quantized model for a digital down converter for LTE (see example).
Quantization in Deep Learning
Quantization for deep learning networks is an important step to help accelerate inference as well as to reduce memory and power consumption on embedded devices. Scaled 8-bit integer quantization maintains the accuracy of the network while reducing the size of the network. This enables deployment to devices with smaller memory footprints, leaving more room for other algorithms and control logic.
Quantization optimizations can be made when the targeted hardware (GPU, FPGA, CPU) architecture is taken into consideration. This includes computing in integers, utilizing hardware accelerators, and fusing layers. The quantization step is an iterative process to achieve acceptable accuracy of the network.
See how to quantize, calibrate, and validate deep neural networks in MATLAB using a white-box approach to make tradeoffs between performance and accuracy, then deploy the quantized DNN to an embedded GPU and an FPGA hardware board.

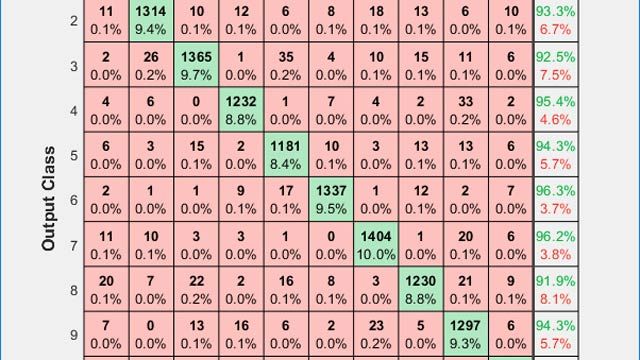
Confusion matrix of the classification rate of a scaled MNIST (read article).
Quantizing a Deep Learning Network in MATLAB
In this video, we demonstrate the deep learning quantization workflow in MATLAB. Using the Model Quantization Library Support Package, we illustrate how you can calibrate, quantize, and validate a deep learning network such as Resnet50.
Deep Learning Network Quantization Library for Deployment to Embedded Targets
Learn about deep network quantization, and what is quantized in the Deep Network Quantizer app. An example semantic segmentation network is shown with deployment to both GPU and CPU.
Deep Network Quantization and Deployment
See how to quantize, calibrate, and validate deep neural networks in MATLAB using a white-box approach.
Deep Learning Toolbox Model Quantization Library
Learn about and download the Deep Learning Toolbox Model Quantization Library support package.
How Quantization Works
Quantization errors are a cumulative effect of non-linear operations like rounding of the fractional part of a signal or overflow of the dynamic range of the signal. You can take quantization errors into account when converting a design for embedded hardware by observing the key signals or variables in your design and budgeting the quantization error so that the numerical difference is within acceptable tolerance.
Quantization with MATLAB and Simulink
With MATLAB and Simulink, you can:
- Explore and analyze the quantization error propagation
- Automatically quantize your design to limited precision
- Debug numerical differences that result from quantization
Explore and Analyze Quantization Errors
You can collect simulation data and statistics through automatic model-wide instrumentation. MATLAB visualizations of this data enable you to explore and analyze your designs to understand how your data type choices affect the underlying signal.

Visualizing the range and precision of the signals from simulation.
Automatically Quantize Your Design
You can quantize your design by selecting a specific data type, or you can iteratively explore different fixed-point data types. Using a guided workflow, you can see the overall effect that quantization has on the numerical behavior of your system.
Alternatively, you can solve the optimization problem and choose the optimal heterogenous data type configuration for your design that meets the tolerance constraints on the numerical behavior of your system.
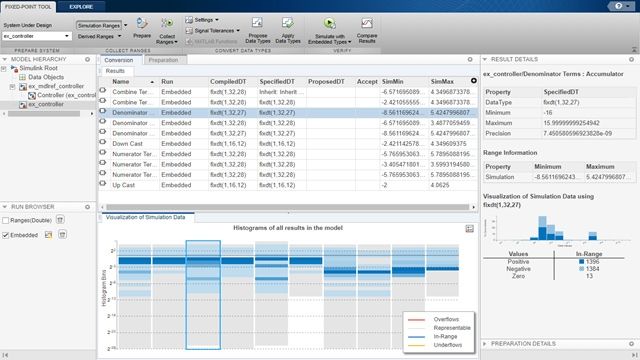
Conversion workflow using the Fixed-Point Tool.
Learn more about fixed-point conversion:
- Converting your Simulink model iteratively using the Fixed-Point Tool
- Automatic conversion using fixed-point optimization
Debug Numerical Differences Due to Quantization
With MATLAB, you can identify, trace, and debug the sources of numerical issues due to quantization such as overflow, precision loss, and wasted range or precision in your design.

Tracing an overflow to the corresponding line in the MATLAB code.
Examples and How To
Software Reference
See also: filter design, motor control design with Simulink, hardware design with MATLAB and Simulink