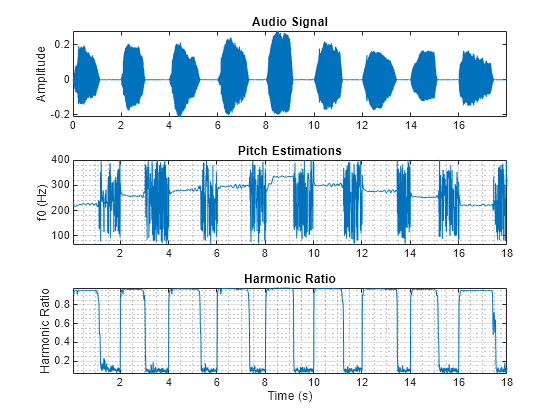
pitch
Estimate fundamental frequency of audio signal
Description
f0 = pitch(audioIn,fs,Name=Value)
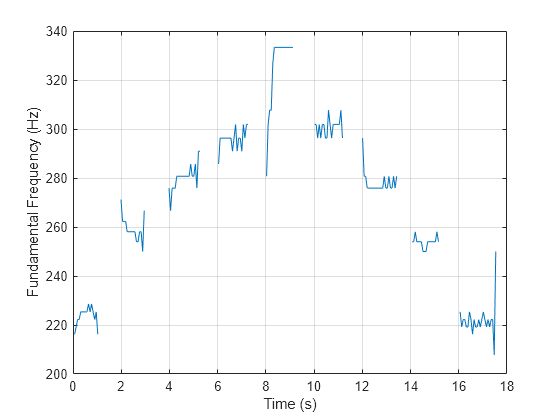
pitch(___) with no output arguments plots the
estimated pitch against time.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
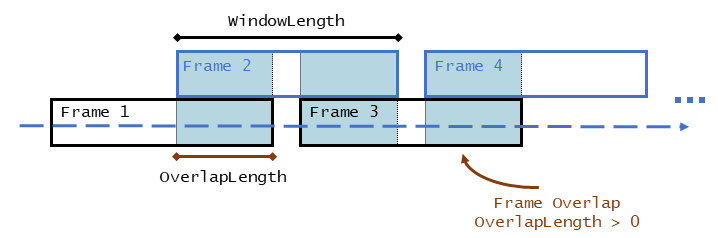
The pitch function segments the audio input according to the
WindowLength and OverlapLength arguments.
The fundamental frequency is estimated for each frame. The locations output,
loc contains the most recent samples (largest sample numbers)
of the corresponding frame.
For a description of the algorithms used to estimate the fundamental frequency, consult the corresponding references:
References
[1] Atal, B.S. "Automatic Speaker Recognition Based on Pitch Contours." The Journal of the Acoustical Society of America. Vol. 52, No. 6B, 1972, pp. 1687–1697.
[2] Gonzalez, Sira, and Mike Brookes. "A Pitch Estimation Filter robust to high levels of noise (PEFAC)." 19th European Signal Processing Conference. Barcelona, 2011, pp. 451–455.
[3] Noll, Michael A. "Cepstrum Pitch Determination." The Journal of the Acoustical Society of America. Vol. 31, No. 2, 1967, pp. 293–309.
[4] Hermes, Dik J. "Measurement of Pitch by Subharmonic Summation." The Journal of the Acoustical Society of America. Vol. 83, No. 1, 1988, pp. 257–264.
[5] Drugman, Thomas, and Abeer Alwan. "Joint Robust Voicing Detection and Pitch Estimation Based on Residual Harmonics." Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH. 2011, pp. 1973–1976.
Extended Capabilities
Version History
Introduced in R2018a