Kasami Sequence Generator
Generate Kasami sequence from set of Kasami sequences
Libraries:
Communications Toolbox /
Comm Sources /
Sequence Generators
Description
The Kasami Sequence Generator block generates a sequence from a set of Kasami sequences. The Kasami sequences are a set of sequences that have good cross-correlation properties. For more information, see Kasami Sequences.
This block can output sequences that vary in length during simulation. For more information about variable-size signals, see Variable-Size Signal Basics (Simulink).
These icons show the block with oSiz, Ref
and Rst ports enabled.
![]()
![]()
Examples
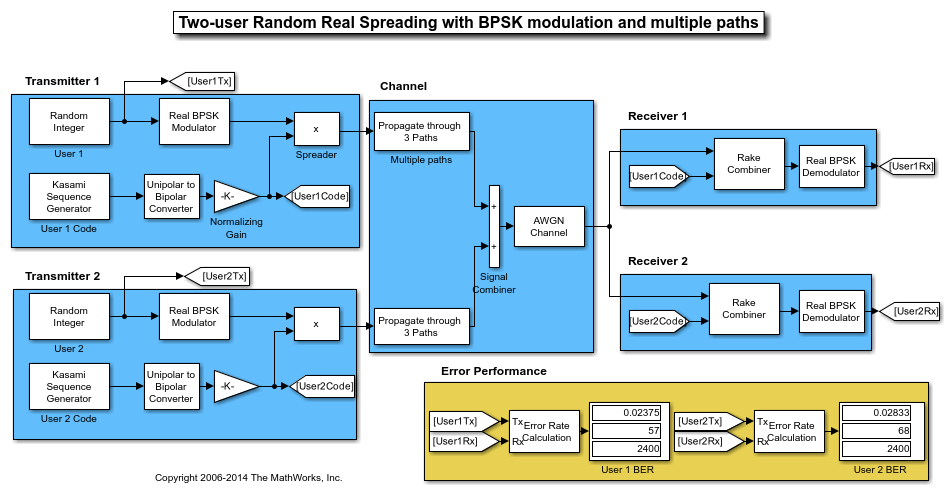
Kasami Spreading for Multiuser System in Multipath Channel
This model simulates Kasami sequence spreading for two users in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.
Ports
Input
Current output size, specified as a scalar or a vector of the form [n,1], where n is the number of elements in the output sequence.
Example: [10 1] a specifies a current output column
vector of size 10-by-1.
Dependencies
To enable this port, set the Maximum output size
source parameter to Dialog
parameter.
Data Types: double
Reference input signal, specified as a scalar, or a column vector.
Dependencies
To enable this port, set the Maximum output size
source parameter to Inherit from
reference input.
Data Types: double
Reset signal, specified as a scalar or vector, depending on the output size.
When the output size is variable, specify this port as a scalar.
Otherwise, specify this port as a scalar or a column vector of length equal to the Samples per frame parameter value.
The output signal resets for nonzero Rst input values. For more information, see Reset Behavior.
Dependencies
To enable this port, select the Reset on nonzero input parameter.
Data Types: double
Output
Output signal, returned as a binary-valued column vector. At least one element of the Initial states parameter vector must be nonzero for the block to generate a nonzero sequence.
Data Types: double
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Specify the generator polynomial, which determines the connections in the shift register that generates the sequence, as one of these options.
A polynomial character vector or string scalar that includes the number
1(for example,'z^4 + z + 1'). For more information, see Representation of Polynomials in Communications Toolbox.A binary-valued row vector that lists the coefficients of a polynomial in order of descending powers. The first and last entries must be
1. The length of this vector must be one more than the degree of the generator polynomial.An integer-valued row vector containing the exponents of the nonzero terms of a polynomial in order of descending powers. The last entry must be
0.
For example, 'z^8 + z^2 + 1', [1 0 0 0 0 0 1 0
1], and [8 2 0] represent the same
polynomial p(z) =
z8 +
z2 + 1.
The initial states of the shift register generate the sequence. If you specify a binary-valued row vector, the length must equal the degree of the generator polynomial specified by the Generator polynomial parameter. If you specify a binary-valued scalar, the block expands the scalar to a row vector of length equal to the degree of the generator polynomial. All entries of the resulting vector equal the scalar.
Specify an integer or vector of the form [k m] to select a Kasami sequence of interest from the set of possible sequences. Two classes of Kasami sequences exist: those obtained from a small set and those obtained from a large set. You can choose a Kasami sequence from the small set by setting this parameter to an integer in the range [0, 2n/2–2]. You can choose a sequence from the large set by setting this parameter to a vector of the form [k m]. k must be an integer in the range [–2, 2n–2], and m must be an integer in the range [–1, 2n/2–2]. For more information, see Sequence Index.
Specify the offset of the Kasami sequence from the initial time.
You can use an external signal to reset the values of the internal shift register to the initial state by selecting the Reset on nonzero input parameter. This selection creates an input port for the external signal in this block. The way the block resets the internal shift register depends on whether its output signal and reset signal are sample-based or frame-based. For an example, see Reset Behavior.
Select this parameter to enable variable-length output sequences during simulation. When you clear this parameter, the block outputs fixed-length sequences. When you select this parameter, the block can output variable-length sequences. For information about variable-size signals, see Variable-Size Signal Basics (Simulink).
Select how to specify the maximum sequence output size.
Dialog parameter— Select this value to configure the block to use the Maximum output size parameter setting as the maximum permitted output sequence length. The oSiz input port specifies the current size of the output signal, and the block output inherits the sample time from the input signal. The input value of oSiz must be less than or equal to the Maximum output size parameter.Inherit from reference port— Select this value to enable the Ref input port and configure the block to inherit the sample time, maximum size, and current output size from the variable-sized signal at the Ref input port. These set the maximum permitted output sequence length.
Dependencies
To enable this parameter, select Output variable-size signals.
Specify the maximum output size for the block. n is a positive scalar.
Example: [10 1] specifies a 10-by-1 maximum size for the output
signal.
Dependencies
To enable this parameter, select Output variable-size
signals and set Maximum output size source to
Dialog parameter.
Positive scalars specify the time in seconds between each
sample of the output signal. If you set the sample time to -1, the output
signal inherits the sample time from downstream. For information on the relationship between the
Sample time and Samples per frame parameters,
see
Sample Timing.
Dependencies
To enable this parameter clear Output variable-size signals.
Specify the number of samples per frame in one channel of the output data. For information on the relationship between the Sample time and Samples per frame parameters, see Sample Timing.
Select this parameter to enable the Rst input port. Use that port to specify an input signal that resets the internal shift registers to the original values of the Initial states parameter value.
Specify the output data type of the block.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
The time between output updates is equal to the product of the
Samples per frame and Sample time parameter
values. For example, if Sample time and Samples per
frame each equal 1, the block outputs one sample every
second. If you increase Samples per frame to 10, then the block outputs
a 10-by-1 vector every 10 seconds. This timing ensures that the equivalent output rate is
not dependent on the Samples per frame parameter.
Two sets of Kasami sequences exist: the small set and the large set. The large set contains all of the sequences in the small set. Only the small set is optimal in the sense of matching Welch's lower bound for correlation functions.
Kasami sequences have a period of N = 2n – 1, where n is a nonnegative even integer. Let u be a binary sequence of length N, and let w be the sequence obtained by decimating u by 2n/2 + 1. This piecewise function defines the small set of Kasami sequences. T is the left shift operator, m is the shift parameter for w, and denotes addition modulo 2.
The small set contains 2n/2 sequences.
For mod(n, 4) = 2, this piecewise function defines the large set of Kasami sequences. Let v be the sequence formed by decimating the sequence u by 2(n/2 + 1) + 1. k and m are the shift parameters for the sequences v and w, respectively.
The sequences described in the first three rows of
KL correspond to the Gold sequences
for mod(n, 4) = 2. For a description of Gold sequences, see the
comm.GoldSequence
System object™ reference page. However, the Kasami sequences form a larger set than
the Gold sequences alone.
The correlation functions for the sequences take on the values
{–t(n), –s(n), –1, s(n) – 2, t(n) – 2},
where
Kasami sequences have a period of N = 2n – 1, where n is a nonnegative even integer. This table lists some of the polynomials that you can use to generate the set of Kasami sequences.
| n | N | Polynomial | Set |
|---|---|---|---|
| 4 | 15 | 'z^4 + z +1' | Small |
| 6 | 63 | 'z^6 + z +1' | Large |
| 8 | 255 | 'z^8 + z^4 + z^3 + z^2 +1' | Small |
| 10 | 1023 | 'z^10 + z^3 +1' | Large |
| 12 | 4095 | 'z^12 + z^6 + z^4 + z +1' | Small |
The Sequence index(es) parameter specifies the shifts of the sequences v and w used to generate the output sequence. You can specify the parameter in one of these two ways.
To generate sequences from the small set, when n is even, you can specify Sequence index(es) as an integer m in the range [–1, 2n/2 – 2]. This table describes the output sequences corresponding to Sequence index(es) values.
Sequence index(es) Value Range of Indices Output Sequence -1m = –1 u m m = 0, 2n/2 – 2 To generate sequences from the large set for mod (n, 4) = 2, where n is the degree of the generator polynomial (set by the Generator polynomial parameter), you can specify Sequence index(es) as a vector of the form [k m]. In this case, the output sequence is from the large set k is an integer in the range [–2, 2n – 2], and m is an integer in the range [–1, 2n/2 – 2]. This table describes the output sequences corresponding to Sequence index(es) values.
Sequence index(es) Value Range of Indices Output Sequence [-2 -1]k = –2
m = –1
u [-1 -1]k = –1
m = –1
v [k –1]k = 0, 1, ..., 2n – 2
m = –1
[-2 m]k = – 2
m = 0, 1, ..., 2n/2 – 2
[-1 m]k = –1
m = 0, ..., 2n/2 –2
[k m]k = 0, ..., 2n –2
m = 0, ..., 2n/2 –2
Before you can reset the generator sequence, you must select the
Reset on nonzero input parameter to enable the
Rst input port. Suppose that the Kasami Sequence Generator block outputs
[1 0 0 1 1 0 1 1] when no reset exists. This table shows the effect
on the Kasami Sequence Generator block output for the parameter values indicated.
| Reset Signal | Reset Signal Settings | Kasami Sequence Generator block | Reset Signal and Output Signal |
|---|---|---|---|
| No reset |
|
|
|
| Scalar reset signal |
|
|
|
| Vector reset signal |
|
|
For the no-reset case, the block outputs the sequence without resetting it.
For the scalar and vector reset signal cases, the block inputs the reset signal [0
0 0 1 0 0 0 0] to the Rst port. Because the fourth bit of
the reset signal is a 1 and Sample time is
1, the block resets the sequence output at the fourth bit.
For variable-sized outputs, the block supports only scalar reset signal inputs.
References
[1] Peterson, W. Wesley, and E. J. Weldon. Error-Correcting Codes. 2d ed. MIT Press, 1972.
[2] Proakis, John G. Digital Communications. 4th ed. New York: McGraw Hill, 2001.
[3] Sarwate, D.V., and M.B. Pursley. “Crosscorrelation Properties of Pseudorandom and Related Sequences.” Proceedings of the IEEE® 68, no. 5 (1980): 593–619. https://doi.org/10.1109/PROC.1980.11697.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006aStarting in R2020a, Simulink no longer allows you to use the Kasami Sequence Generator block version available before R2015b.
Existing models automatically update to load the Kasami Sequence Generator block version announced in Source blocks output frames of contiguous time samples but do not use frame attribute. For more information on block forwarding, see Maintain Compatibility of Library Blocks Using Forwarding Tables (Simulink).
See Also
Blocks
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)