Accelerate MIMO-OFDM Link Simulation Using GPU
This example shows how to accelerate a multiple input multiple output (MIMO) link simulation that uses orthogonal frequency division multiplexing (OFDM) and low-density parity-check (LDPC) channel coding. To accelerate the simulation, the example uses a graphical processing unit (GPU).
In this example, you learn how to run a MIMO-OFDM link simulation on the GPU by generating the transmitted data bits as gpuArray (Parallel Computing Toolbox) objects. Then you compare the acceleration that you gain by using a single GPU versus a parallel pool of CPU workers against using just one CPU worker.
Introduction
Because many functions in MATLAB® automatically run on a GPU if you supply a gpuArray data argument, you can accelerate the simulation simply by generating the information bits as a gpuArray. A gpuArray object represents an array stored in the GPU memory. In this simulation, the gpuArray objects flow through each link component executing its computations on the GPU. Using a GPU can accelerate a wireless link simulation if the link components have a high number of computations that the simulation can execute in parallel.

The example compares run-time performance of simulating one bit error rate (BER) point while running on:
A single CPU worker
A pool of CPU workers
A single GPU
This example is published using an Intel® Xeon® Gold 5415+ CPU and an NVIDIA® H100 PCIe GPU. The acceleration results may vary based on the available hardware resources.
The timing results show that when each component in the system has a high number of parallelizable computations, the simulation can achieve the following acceleration factors when compared to a single CPU worker:
A pool of 8 CPU workers: up to a factor of 4.
A single GPU: up to a factor of 55.
In the next section, you learn how to run the link simulation for one iteration on the GPU. Afterward, you see how using GPU processing becomes more beneficial when the simulation is set up to execute a large number of calculations in parallel.
Detect GPU
Verify that a supported GPU is available for computation.
if canUseGPU gpuExist = true; D = gpuDevice; fprintf('GPU detected, %s Device, %d multiprocessors, %s compute capability.\n', ... D.Name, D.MultiprocessorCount, D.ComputeCapability); else gpuExist = false; warning(['Could not find an appropriate GPU. ' ... 'The example will skip all GPU simulations.']); end
GPU detected, NVIDIA H100 PCIe Device, 114 multiprocessors, 9.0 compute capability.
Set Simulation Parameters
In a wireless communications link, GPU processing can be useful for simulating a system with many transmit or receive antennas, encoding multiple codewords in parallel, modulating many OFDM symbols or simulating a fading channel with many fading paths. Start by simulating a link with a short LDPC block length of 648 bits, 2 transmit (Tx) antennas, 2 receive (Rx) antennas, and 20 codewords per frame. In the later sections, you see how a system with higher parameters achieves higher GPU utilization and a higher acceleration factor.
MIMO and Beamforming Matrix
Set the number of transmitted data streams to 1. Map the data streams to 2 antennas using an analog beamforming matrix with consecutive phase shifters.
numTx =2; numRx =
2; numStreams =
1; fc = 1e9; lambda = physconst('LightSpeed')/fc; beamAngles = 15; antIdx = 0:numTx-1; antDelay = 2*pi*sin(2*pi*beamAngles*(0:numStreams-1).'/360)/lambda; B = single(exp(1i*antIdx.*antDelay));
Channel Coding
Use a 16-QAM modulator and transmit 20 LDPC codewords in each frame. Use an LDPC encoder with coding rate and block length 648.
numBitsPerCarrier =4; numCWPerFrame =
20; crcCfg = crcConfig; ldpcEncCfg = ldpcEncoderConfig; ldpcDecCfg = ldpcDecoderConfig; numMsgBits = ldpcEncCfg.NumInformationBits-16; modOrder = 2^numBitsPerCarrier;
OFDM Modulation
Set the FFT length to 512, set the cyclic prefix length to 64, and use 20 null subcarriers for the guard band on each side.
fftLength =512; cpLength = fftLength/8; ofdmNullIdx = [1:19 ( fftLength/2+1) (fftLength-19: fftLength)]'; % Guard bands and DC subcarrier numDataSC = fftLength-length(ofdmNullIdx); activeIdx = setdiff(1:fftLength,ofdmNullIdx); numOFDMSym = ceil(numCWPerFrame * ldpcEncCfg.BlockLength / numBitsPerCarrier / numDataSC/ numStreams); paddingSymbols = (numDataSC - mod(numCWPerFrame * ldpcEncCfg.BlockLength / numBitsPerCarrier,numDataSC));
Fading Channel and AWGN
Set the energy per bit to noise power ratio (EbNo) to 0 dB. Set the subcarrier spacing to 60 KHz and the maximum Doppler shift to 100 Hz. Use a Rayleigh fading channel with 24 fading paths.
EbNodB =0; snrdB = convertSNR(EbNodB,"ebno", ... BitsPerSymbol=numBitsPerCarrier, ... CodingRate=ldpcEncCfg.CodeRate); SCS = 60; fs = SCS*1e3*fftLength/0.85; maxDoppler = 100; pathDelays = [0.0000 0.2099 0.2219 0.2329 0.2176 ... 0.6366 0.6448 0.6560 0.6584 0.7935 ... 0.8213 0.9336 1.2285 1.3083 2.1704 ... 2.7105 4.2589 4.6003 5.4902 5.6077 ... 6.3065 6.6374 7.0427 8.6523]; % TDL-C delay profile delaySpread = 100*1e-9; % (ns) avgPathGains = [-4.4 -1.2 -3.5 -5.2 -2.5 ... 0.0 -2.2 -3.9 -7.4 -7.1 ... -10.7 -11.1 -5.1 -6.8 -8.7 .... -13.2 -13.9 -13.9 -15.8 -17.1 .... -16.0 -15.7 -21.6 -22.8]; % TDL-C delay profile mimoChannel = comm.MIMOChannel( ... SampleRate=fs, ... PathDelays=pathDelays*delaySpread, ... AveragePathGains=avgPathGains, ... SpatialCorrelationSpecification="None", ... NumTransmitAntennas=numTx, ... NumReceiveAntennas=numRx, ... MaximumDopplerShift=maxDoppler, ... PathGainsOutputPort=true,... FadingTechnique="Sum of sinusoids", ... NormalizeChannelOutputs=false);
Simulate OFDM-MIMO Link Using GPU
By generating the initial data on the GPU and without making any further modifications to your code, all subsequent computations happen on the GPU. Measure the run time of one instance of the link on the GPU by using the tic and toc functions.
if gpuExist tStart = tic; % Generate information bits msg = randi([0 1],numMsgBits,numCWPerFrame,"int8","gpuArray"); % Channel coding crcgen = crcGenerate(msg, crcCfg); encldpc = ldpcEncode(crcgen,ldpcEncCfg); % Modulation modsymbols = qammod(encldpc, modOrder, ... InputType="bit", ... UnitAveragePower=true, ... OutputDataType="single"); txSigScaling = (fftLength/sqrt( numDataSC)); ofdmdata = txSigScaling*ofdmmod(reshape([modsymbols(:); ... zeros(paddingSymbols,1)],numDataSC,numOFDMSym,numStreams), ... fftLength,cpLength,ofdmNullIdx); % Beamforming txsig = ofdmdata*B; % Fading channel with AWGN [channelout,pathgains] = mimoChannel(txsig); sigpowerdB = 10.*log10((numTx/numStreams)/numRx); [rxsig, nvar] = awgn(channelout,snrdB,sigpowerdB); pathfilters = info(mimoChannel).ChannelFilterCoefficients; timingoffset = info(mimoChannel).ChannelFilterDelay; % Perfect channel estimation Hest = ofdmChannelResponse(pathgains,pathfilters,fftLength, ... cpLength,activeIdx,timingoffset); H = reshape(Hest,[],numTx,numRx); % OFDM demodulation % Handle timing offset before OFDM demodulation: % Remove initial samples and pad zeros to keep signal length unchanged shiftedSig = (sqrt(numDataSC) / fftLength)* ... [rxsig(timingoffset+1:end,:); zeros(timingoffset, numRx)]; % Sampling offset for OFDM demodulation symoffset = cpLength/2; % The padded zeros are not used if timingOffset <= cpLen/2 dmodofdm = ofdmdemod(shiftedSig,fftLength,cpLength,symoffset,ofdmNullIdx); % Frequency domain equalization heffperm = pagemtimes( B, permute(H, [2,3,1])); heff = permute(heffperm, [3, 1, 2]); eqsym = ofdmEqualize(dmodofdm,heff,nvar,Algorithm="mmse"); eqsym(end- paddingSymbols+1:end) = []; % QAM demodulation dmodqam = qamdemod(reshape(eqsym,ldpcEncCfg.BlockLength/numBitsPerCarrier,[]),... modOrder,UnitAveragePower=true,OutputType="approxllr",NoiseVariance=nvar); % Decoding decldpc = ldpcDecode(dmodqam,ldpcDecCfg,10,Termination="max"); crcdet = crcDetect(decldpc, crcCfg);
To ensure that all the GPU computations are complete, you must call wait (Parallel Computing Toolbox) before calling toc.
wait(D); toc(tStart) % Error rate calculations numBitErrors = biterr(msg, crcdet) numBlockErrors = sum(biterr(msg, crcdet,"column-wise")>0)
Note that the gpuArray objects pass throughout the link executing every component on the GPU.
isgpuarray(crcdet)
endElapsed time is 0.133441 seconds.
numBitErrors = 770
numBlockErrors =
20
ans = logical
1
Accelerate Link Using GPU Versus parfor-Loop
In this section, you simulate the link on the CPU, on a parallel pool of CPU workers, and on a single GPU. Then you compare the run time, BER, and BLER of each simulation.
maxNumFrames =  10000;
simParam = helperLinkSetup(numTx,numRx,numStreams,numBitsPerCarrier,numCWPerFrame,fftLength);
10000;
simParam = helperLinkSetup(numTx,numRx,numStreams,numBitsPerCarrier,numCWPerFrame,fftLength);To run the link on the CPU, set UseGPU flag in the simParam structure to false. The helperLDPCMIMOOFDMSimulation function simulates the link for maxNumFrames.
simParam.UseGPU = false;
simOutputCPU = helperLDPCMIMOOFDMSimulation(maxNumFrames,EbNodB,simParam);
false;
simOutputCPU = helperLDPCMIMOOFDMSimulation(maxNumFrames,EbNodB,simParam);Start simulating link on the CPU ... Simulation on the CPU is DONE.
parfor-Loop Parallelization Strategy
Use the helperLDPCMIMOOFDMSimulationParfor function to run the same simulation on a pool of parallel CPU workers. The function uses the existing parallel pool if one is open. Otherwise, it opens one with the default parallel profile.
To achieve high acceleration for BLER Monte-Carlo simulations with the parfor (Parallel Computing Toolbox) function, distribute the maximum number of iterations evenly across the parallel workers for all EbNo values. Otherwise, if you set each worker to run all iterations for one EbNo value, the acceleration factor is limited by the run time of the highest EbNo value until the specified number of errors occurs. For a comparison between the two parallelization techniques, see Simulation Acceleration Using MATLAB Coder and Parallel Computing Toolbox.
simOutputParfor = helperLDPCMIMOOFDMSimulationParfor(maxNumFrames, ...
EbNodB,simParam);Start simulating link using parfor using 8 workers ... Simulation using parfor is DONE.
GPU Parallelization Strategy
To run the link on the GPU, set the UseGPU flag in the simParam structure to true. With no other modifications to the helperLDPCMIMOOFDMSimulation function, it generates the information bits as gpuArray objects executing the link on the GPU.
if gpuExist simParam.UseGPU =true; simParam.Device = D; simOutputGPU = helperLDPCMIMOOFDMSimulation(maxNumFrames,EbNodB,simParam); end
Start simulating link on the GPU ... Simulation on the GPU is DONE.
simToCompare = [simOutputCPU,simOutputParfor,simOutputGPU];
Speed-up Results
Use helperCompareSimulatedLinks function to compare the BER, BLER and run time of each simulation. The GPU accelerates the simulation with a factor of 2.72 whereas the parallel pool of 8 CPU workers offers an acceleration factor of 4.18. In the next section, you see how the GPU acceleration factor increases when simulating a highly parallelizable system.
For reproducibility, the helperLDPCMIMOOFDMSimulation function fixes the random number generator algorithm, seed, and normal transformation on the CPU and the GPU. For details on random number generators supported in both environments, see Random Number Streams on a GPU (Parallel Computing Toolbox). The parfor loop, however, uses a different random number stream on each worker resulting in slightly different results. For additional details, see Control Random Number Streams on Workers (Parallel Computing Toolbox).
helperCompareSimulatedLinks(simToCompare,EbNodB);
-------------------------------------------------------------------------------------------------------------------------------- Environment | EbNo(dB)| BER | Num Bits | BLER | Num Blocks | Elapsed Time(sec) | Speed-up factor -------------------------------------------------------------------------------------------------------------------------------- CPU | 0.00 | 6.6684e-02 | 104810480 | 8.6009e-01 | 200020 | 220.65 | 1.00 parfor | 0.00 | 6.3264e-02 | 104800000 | 8.3759e-01 | 200000 | 52.80 | 4.18 GPU | 0.00 | 6.6684e-02 | 104810480 | 8.6009e-01 | 200020 | 81.17 | 2.72
Accelerate Link with Highly Parallelizable Components
Increase the number of transmit antennas to 64, the number of receive antennas to 8 and the number of codewords per frame to 50. Set the number of bits per carrier to 8 and EbNo to -3 dB. You see how the GPU can accelerate the link simulation with a higher factor as you increase its utilization. Set the maxNumFrames to 2000.
maxNumFrames = 2000; EbNodB = -3; numCWPerFrame =50; numStreams =
1; numBitsPerCarrier =
8; numTx =
64; numRx =
8; simParam = helperLinkSetup(numTx,numRx,numStreams,numBitsPerCarrier,numCWPerFrame,fftLength);
Running this section on the CPU takes a long time. By default, the example loads presaved results for the simulation using the CPU and parfor loop. To run the simulation, set the runNow flag to true. It could take more than 30 minutes to complete.
runNow =false; if ~runNow load simulationResultsCPU.mat else simParam.UseGPU =
false; %#ok<UNRCH> simOutputCPU = helperLDPCMIMOOFDMSimulation(maxNumFrames,EbNodB,simParam); simOutputParfor = helperLDPCMIMOOFDMSimulationParfor(maxNumFrames, ... EbNodB,simParam); end simToCompare = [simOutputCPU, simOutputParfor];
To run the link on the GPU, set the UseGPU flag in the simParam structure to true.
if gpuExist simParam.UseGPU =true; simParam.Device = D; simOutputGPU = helperLDPCMIMOOFDMSimulation(maxNumFrames,EbNodB,simParam); simToCompare = [simToCompare, simOutputGPU]; end
Start simulating link on the GPU ... Simulation on the GPU is DONE.
Speedup Results
Use the helperCompareSimulatedLinks to compare the simulation results. The GPU shows the highest acceleration factor of 55.3 when compared to using the parallel pool of 8 CPU workers, which provides an acceleration factor of approximately 3.2. This gain is expected since the GPU parallelizes the computations within each component of the simulated link rather than parallelizing over the simulation iterations.
helperCompareSimulatedLinks(simToCompare,EbNodB);
-------------------------------------------------------------------------------------------------------------------------------- Environment | EbNo(dB)| BER | Num Bits | BLER | Num Blocks | Elapsed Time(sec) | Speed-up factor -------------------------------------------------------------------------------------------------------------------------------- CPU | -3.00 | 1.0859e-02 | 52426200 | 3.0980e-01 | 100050 | 1336.75 | 1.00 parfor | -3.00 | 7.0527e-03 | 52400000 | 2.0815e-01 | 100000 | 422.23 | 3.17 GPU | -3.00 | 1.0860e-02 | 52426200 | 3.0980e-01 | 100050 | 24.16 | 55.33
Compare BLER Curves
Compare the BLER of the previous section for EbNo values ranging between -4 and 0 dB. The CPU and GPU curves are identical because the simulation for the CPU and the GPU each use the same random number generator. The curve for the parfor loop is slightly different because every worker in the parallel pool uses a different random number stream.
To regenerate these curves, set the following parameters and rerun the previous section:
EbNodB = -4 : 0
maxNumFrames = (1 : 2 : 10)*1e3

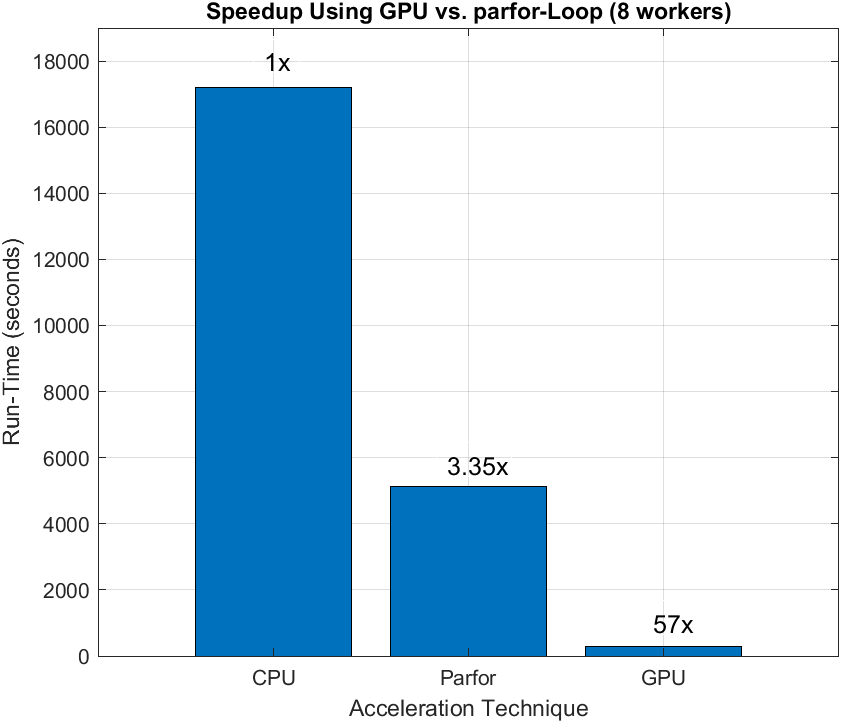
Now compare the run times of the BLER simulations. The CPU takes >17000 seconds (4.7 hours) and the parallel pool of 8 CPU workers takes about 1500 seconds (1.4 hours), achieving a speedup factor of 3.35. Finally, the GPU takes about 300 seconds (5 minutes) with a speedup factor of 57 for simulating the same BLER curve without losing any numeric accuracy compared to the CPU. From this plot, you see that using the GPU for systems with highly parallelizable components achieves higher acceleration gains.
Helper Functions
helperLinkSetup.m
helperLDPCMIMOOFDMSimulation.m
helperLDPCMIMOOFDMSimulationParfor.m
helperTransmissionLink.m
helperCompareSimulatedLinks.m
See Also
RandStream | parallel.gpu.RandStream (Parallel Computing Toolbox) | gpurng (Parallel Computing Toolbox)
Topics
- Identify and Select a GPU Device (Parallel Computing Toolbox)
- Establish Arrays on a GPU (Parallel Computing Toolbox)
- Measure and Improve GPU Performance (Parallel Computing Toolbox)