Passive Control with Communication Delays
This example shows how to mitigate communication delays in a passive control system.
Passivity-Based Control
By the Passivity Theorem, the negative-feedback interconnection of two strictly passive systems 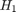 and
and  is always stable.
is always stable.

When the physical plant is passive, it is therefore advantageous to use a passive controller for robustness and safety reasons. In networked control systems, however, communication delays can undo the benefits of passivity-based control and lead to instability. To illustrate this point, we use the plant and 2nd-order passive controller from the "Vibration Control in Flexible Beam" example. See this example for background on the underlying control problem. Load the plant model 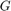 and passive controller
and passive controller  (note that
(note that  corresponds to
corresponds to 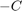 in the other example).
in the other example).
load BeamControl G C bode(G,C,{1e-2,1e4}) legend('G','C')

The control configuration is shown below as well as the impulse response from  to
to 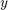 .
.

impulse(feedback(G,C))

Destabilizing Effect of Communication Delays
Now suppose there are substantial communication delays between the sensor and the controller, and between the controller and the actuator. This situation is modeled in Simulink® as follows.
open_system('DelayedFeedback')

The communication delays are set to
T1 = 1; T2 = 2;
Simulating this model shows that the communication delays destabilize the feedback loop.

Scattering Transformation
To mitigate the delay effects, you can use a simple linear transformation of the signals exchanged between the plant and controller over the network.

Figure 1: Networked Control System
This is called the "scattering transformation" and given by the formulas
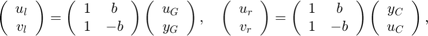
or equivalently

with  . Note that in the absence of delays, the two scattering transformations cancel each other and the block diagram in Figure 1 is equivalent to the negative feedback interconnection of
. Note that in the absence of delays, the two scattering transformations cancel each other and the block diagram in Figure 1 is equivalent to the negative feedback interconnection of 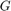 and
and  .
.
When delays are present, however,  is no longer equal to
is no longer equal to 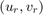 and this scattering transformation alters the properties of the closed-loop system. In fact, observing that
and this scattering transformation alters the properties of the closed-loop system. In fact, observing that
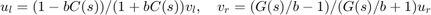
and that 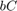 and
and 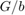 strictly passive ensures that
strictly passive ensures that
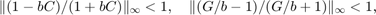
the Small Gain Theorem guarantees that the feedback interconnection of Figure 1 is always stable no matter how large the delays. Confirm this by building a Simulink model of the block diagram in Figure 1 for the value 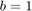 .
.
b = 1;
open_system('ScatteringTransformation')

Simulate the impulse response of the closed-loop system as done before. The response is now stable and similar to the delay-free response in spite of the large delays.

For more details on the scattering transformation, see T. Matiakis, S. Hirche, and M. Buss, "Independent-of-Delay Stability of Nonlinear Networked Control Systems by Scattering Transformation," Proceedings of the 2006 American Control Conference, 2006, pp. 2801-2806.