mfilt.iirdecim
IIR decimator
Compatibility
Note
mfilt.iirdecim will be removed in a future release. Use
dsp.IIRHalfbandDecimator instead.
Syntax
hm = mfilt.iirdecim(c1,c2,...)
Description
hm = mfilt.iirdecim(c1,c2,...) constructs an
IIR decimator filter given the coefficients specified in the cell arrays
c1, c2, and so on. The resulting IIR decimator
is a polyphase IIR filter where each phase is a cascade allpass IIR filter.
Each cell array ci contains a set of vectors representing a cascade
of allpass sections. Each element in one cell array is one section. For more information
about the contents of each cell array, refer to
dfilt.cascadeallpass. The contents of the cell arrays are the
same for both filter constructors and mfilt.iirdecim interprets them
same way as mfilt.cascadeallpass.
The following exception applies to interpreting the contents of a cell array —
if one of the cell arrays ci contains only one vector, and that
vector comprises a series of 0s and one element equal to 1, that cell array represents
a dfilt.delay section with latency equal to the number of
zeros, rather than a dfilt.cascadeallpass section. This exception
case occurs with quasi-linear phase IIR decimators.
Although the first example shows how to construct an IIR decimators explicitly, one usually constructs an IIR decimators filter as a result of designing an decimators, as shown in the subsequent examples.
Examples
When the coefficients are known, you can construct the IIR decimator directly using
mfilt.iirdecim. For example, if the filter's coefficients are
[0.6 0.5] for the first phase in the first stage, 0.7 for the second phase in the first
stage and 0.8 for the third phase in the first stage; as well as 0.5 for the first phase
in the second stage and 0.4 for the second phase in the second stage, construct the
filter as shown here.
Hm = mfilt.iirdecim({[0.6 0.5] 0.7 0.8},{0.5 0.4})
Also refer to the “Quasi-Linear Phase Halfband and Dyadic Halfband Designs” section of the “IIR Polyphase Filter Design” example, IIR Halfband Stages in Multistage Filter Design example.
When the coefficients are not known, use the approach given by the following set of examples. Start by designing an elliptic halfband decimator with a decimation factor of 2. The example specifies the optional sampling frequency argument.
tw = 100; % Transition width of filter. ast = 80; % Stopband attenuation of filter. fs = 2000; % Sampling frequency of signal to filter. m = 2; % Decimation factor. hm = fdesign.decimator(m,'halfband','tw,ast',tw,ast,fs);
hm contains the specifications for a decimator defined by
tw, ast, m, and
fs.
Use the specification object hm to design a
mfilt.iirdecim filter object.
d = design(hm,'ellip','filterstructure','iirdecim'); % Note that realizemdl requires Simulink realizemdl(d) % Build model of the filter.
Designing a linear phase decimator is similar to the previous example. In this case, design a halfband linear phase decimator with decimation factor of 2.
tw = 100; % Transition width of filter. ast = 60; % Stopband attenuation of filter. fs = 2000; % Sampling frequency of signal to filter. m = 2; % Decimation factor.
Create a specification object for the decimator.
hm = fdesign.decimator(m,'halfband','tw,ast',tw,ast,fs);
Finally, design the filter d.
d = design(hm,'iirlinphase','filterstructure','iirdecim'); % Note that realizemdl requires Simulink realizemdl(d) % Build model of the filter.
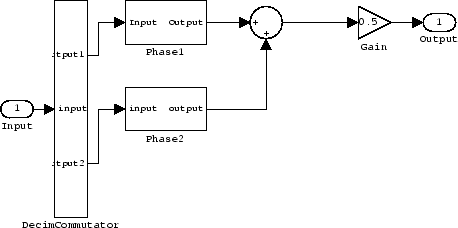
The filter implementation appears in this model, generated by realizemdl and Simulink®.
Given the design specifications shown here
the first phase is a delay section with 0s and a 1 for coefficients and the second phase is a linear phase decimator, shown in the next models.
Phase 1 model
![]()
Phase 2 model

Overall model
Version History
Introduced in R2011a