crosscorr
Sample cross-correlation
Syntax
Description
[
returns the sample cross-correlation
function (XCF) and associated lags between two input vectors of
univariate time series data.xcf,lags] = crosscorr(y1,y2)
XCFTbl = crosscorr(Tbl)DataVariables name-value argument. (since R2022a)
[___, uses any input-argument combination in the
previous syntaxes, and returns the output-argument combination for the
corresponding input arguments and the approximate upper and lower confidence
bounds on the XCF.bounds]
= crosscorr(___)
[___] = crosscorr(___,
uses additional options specified by one or more name-value arguments. For
example, Name=Value)crosscorr(Tbl,DataVariables=["RGDP"
"CPI"],NumLags=10,NumSTD=1.96) returns the sample XCF for lags -10
through 10 of the table variables "RGDP" and
"CPI" in Tbl and 95% confidence
bounds.
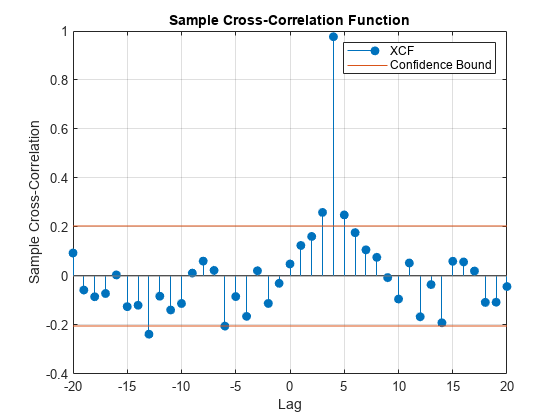
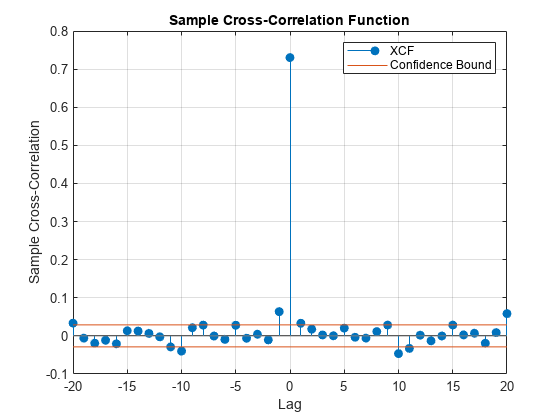
crosscorr(___) plots the sample XCF between
the input series with confidence bounds.
crosscorr(
plots on the axes specified by ax,___)ax instead of
the current axes (gca). ax can precede any of the input
argument combinations in the previous syntaxes.
[___, plots the sample XCF between the input
series and additionally returns handles to plotted graphics objects. Use
elements of h]
= crosscorr(___)h to modify properties of the plot after you
create it.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
If
y1andy2have different lengths,crosscorrappends enough zeros to the end of the shorter vector to make both vectors the same size.crosscorruses a Fourier transform (fft) to compute the XCF in the frequency domain, and thencrosscorrconverts back to the time domain using an inverse Fourier transform (ifft).NaNvalues in the input series result inNaNvalues in the output XCF. Unlikeautocorrandparcorr,crosscorrdoes not treatNaNvalues as missing completely at random. Whereasautocorrandparcorrcompute coefficients in the time domain,crosscorrusesfftandifftto compute coefficients in the frequency domain. Therefore, missing data treatments followfftandifftdefaults.crosscorrplots the XCF when you do not request any output or when you request the fourth output.
References
[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.